题目内容
6. 如图,点F是正方形ABCD的边BC上一点,以BF为对角线作正方形BEFG,连接AG,CE.
如图,点F是正方形ABCD的边BC上一点,以BF为对角线作正方形BEFG,连接AG,CE.(1)求证:AG=CE;
(2)若AD=4,GF=$\sqrt{2}$,求CE的长.
分析 (1)欲证明AG=CE,只要证明△ABG≌△CBE即可.
(2)作GM⊥AB于M,求出MG、AM,在RT△AMG中利用勾股定理即可解决问题.
解答 (1)证明: ∵四边形ABCD是正方形,四边形BEFG是正方形,
∵四边形ABCD是正方形,四边形BEFG是正方形,
∴AB=BC,BG=BE,∠ABC=∠GBE=90°,
∴∠ABG=∠EBC,
在△ABG和△CBE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABG=∠CBE}\\{BG=BE}\end{array}\right.$,
∴△ABG≌△CBE,
∴AG=CE.
(2)解:作GM⊥AB于M.
∵∠ABG=∠GBF=45°,
∴∠MBG=∠MGB=45°,
∵BG=GF=$\sqrt{2}$,AD=AB=4,
∴BM=MG=1,AM=AB-BM=3,
∴AG=CE=$\sqrt{A{M}^{2}+M{G}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
∴CE=$\sqrt{10}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,构造直角三角形,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.适合下列条件的△ABC中,∠A,∠B,∠C是三个内角,a,b,c分别是∠A,∠B,∠C的对边,直角三角形的个数是( )
①a=7,b=24,C=25;
②a=1.5,b=2,c=7.5;
③∠A:∠B:∠C=1:2:3.
④a=1,b=$\sqrt{2}$,c=$\sqrt{3}$.
①a=7,b=24,C=25;
②a=1.5,b=2,c=7.5;
③∠A:∠B:∠C=1:2:3.
④a=1,b=$\sqrt{2}$,c=$\sqrt{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.已知一次函数y=(1+2m)x-1中,函数值y随自变量x的增大而减小,那么m取值范围是( )
| A. | m<-$\frac{1}{2}$ | B. | m≥-$\frac{1}{2}$ | C. | m≤-$\frac{1}{2}$ | D. | m>-$\frac{1}{2}$ |
1.在函数y=$\sqrt{2+x}$中,自变量x的取值范围是( )
| A. | x≥-2 | B. | x≤-2 | C. | x>-2 | D. | x<-2 |
11.若点P(3,2-m)在函数y=$\frac{1}{x}$的图象上,则点P一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.(x3)2的计算结果是( )
| A. | x9 | B. | x6 | C. | x5 | D. | x |
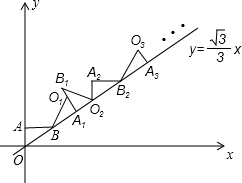 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=$\frac{\sqrt{3}}{3}$x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是($\sqrt{3}$,1),则点A8的横坐标是6$\sqrt{3}$+6.
如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=$\frac{\sqrt{3}}{3}$x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是($\sqrt{3}$,1),则点A8的横坐标是6$\sqrt{3}$+6.