Question

16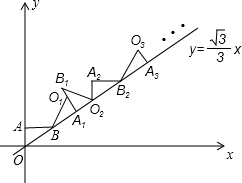．如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A₁BO₁的位置，使点A的对应点A₁落在直线y=$\frac{\sqrt{3}}{3}$x上，再将△A₁BO₁绕点A₁顺时针旋转到△A₁B₁O₂的位置，使点O₁的对应点O₂落在直线y=$\frac{\sqrt{3}}{3}$x上，依次进行下去…，若点A的坐标是（0，1），点B的坐标是（$\sqrt{3}$，1），则点A₈的横坐标是6$\sqrt{3}$+6．

Answer 1

分析 先求出点A₂，A₄，A₆…的横坐标，探究规律即可解决问题．

解答 解：由题意点A₂的横坐标$\frac{3}{2}$（$\sqrt{3}$+1），
点A₄的横坐标3（$\sqrt{3}$+1），
点A₆的横坐标$\frac{9}{2}$（$\sqrt{3}$+1），
点A₈的横坐标6（$\sqrt{3}$+1）．
故答案为6$\sqrt{3}$+6．

点评 本题考查坐标与图形的变换-旋转，一次函数图形与几何变换等知识，解题的关键是学会从特殊到一般，探究规律，由规律解决问题，属于中考常考题型．