题目内容
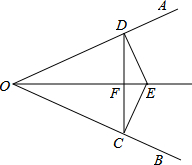 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.(1)求证:OD=OC;
(2)若∠AOB=60°,求证:OE=4EF.
考点:全等三角形的判定与性质,角平分线的性质,含30度角的直角三角形
专题:证明题
分析:(1)利用角平分线定理得到ED=EC,再由斜边为公共边,利用HL得到直角三角形ODE与直角三角形OCE全等,利用全等三角形的对应边相等即可得证;
(2)由OE为角平分线,且∠AOB=60°,得到∠DOE=∠EDF=30°,在直角三角形ODE中,利用30度角所对的直角边等于斜边的一半得到OE=2DE,在直角三角形DEF中,利用30度角所对的直角边等于斜边的一半得到DE=2EF,等量代换即可得证.
(2)由OE为角平分线,且∠AOB=60°,得到∠DOE=∠EDF=30°,在直角三角形ODE中,利用30度角所对的直角边等于斜边的一半得到OE=2DE,在直角三角形DEF中,利用30度角所对的直角边等于斜边的一半得到DE=2EF,等量代换即可得证.
解答:证明:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴ED=EC,
在Rt△ODE和Rt△OCE中,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC;
(2)∵∠AOB=60°,OE平分∠AOB,
∴∠DOE=∠COE=30°,
∴∠DEO=60°,∠EDF=30°,
∵在Rt△ODE中,∠DOE=30°,
∴OE=2DE,
∵在Rt△DEF中,∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
∴ED=EC,
在Rt△ODE和Rt△OCE中,
|
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC;
(2)∵∠AOB=60°,OE平分∠AOB,
∴∠DOE=∠COE=30°,
∴∠DEO=60°,∠EDF=30°,
∵在Rt△ODE中,∠DOE=30°,
∴OE=2DE,
∵在Rt△DEF中,∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列4个命题:①矩形的对角线互相平分且相等;②对角线互相垂直的四边形是菱形;③等腰梯形的两条对角线相等;④等腰三角形底边上的中点到两腰的距离相等.其中正确的是( )
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
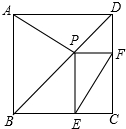
 如图是函数y=x与y=
如图是函数y=x与y= 如图所示,OB,OC分别平分∠ABC,∠ACB,且∠BOC=128°,则∠A=
如图所示,OB,OC分别平分∠ABC,∠ACB,且∠BOC=128°,则∠A=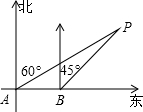 如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据
如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据 已知,如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.
已知,如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.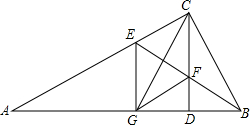 Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.