题目内容
 如图所示,OB,OC分别平分∠ABC,∠ACB,且∠BOC=128°,则∠A=
如图所示,OB,OC分别平分∠ABC,∠ACB,且∠BOC=128°,则∠A=考点:三角形内角和定理
专题:
分析:根据角平分线的定义求出∠OBC、∠OCB,然后利用三角形的内角和等于180°列式计算即可得解.
解答:解:∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×(180°-∠A),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-
×(180°-∠A)=90°+
∠A,
∴∠A=2∠BOC-180°.
∵∠BOC=128°,
∴∠A=76°.
故答案是:76°.
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A=2∠BOC-180°.
∵∠BOC=128°,
∴∠A=76°.
故答案是:76°.
点评:本题考查了三角形的内角和定理,角平分线的定义,熟记定理与概念并准确识图是解题的关键,难点在于整体思想的利用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是( )
如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是( )| A、13 | B、10 | C、12 | D、5 |
 如图:
如图: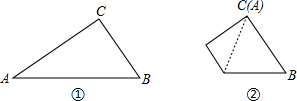 如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);
如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);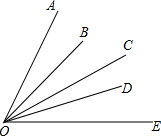 如图所示,五条射线OA、OB、OC、OD、OE组成的图形中共有几个角(小于90°)?如果从O点引出n条射线(最大角为锐角),能有多少个角(小于90°)?你能找出规律吗?
如图所示,五条射线OA、OB、OC、OD、OE组成的图形中共有几个角(小于90°)?如果从O点引出n条射线(最大角为锐角),能有多少个角(小于90°)?你能找出规律吗? 如图,△ABC中AB=AC,∠ABC=45°,AD⊥BC,⊙O经过A,B,D三点,求证:AC是⊙O的切线.
如图,△ABC中AB=AC,∠ABC=45°,AD⊥BC,⊙O经过A,B,D三点,求证:AC是⊙O的切线.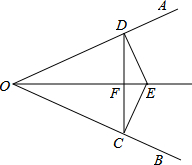 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.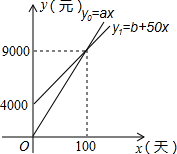 国家推行“节能减排,低碳经济”的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元.据市场调查知:每辆车改装前、后的燃料费(含改装费)(单位:元)与正常运营时间x(单位:天)之间分别满足关系式:y0=ax,y1=b+59x,其图象如图所示.根据图象解决下列问题:
国家推行“节能减排,低碳经济”的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元.据市场调查知:每辆车改装前、后的燃料费(含改装费)(单位:元)与正常运营时间x(单位:天)之间分别满足关系式:y0=ax,y1=b+59x,其图象如图所示.根据图象解决下列问题: 如图,六边形ABCDEF的每个内角都是120°,且AF=AB=3,BC=CD=2,求DE与EF的长.
如图,六边形ABCDEF的每个内角都是120°,且AF=AB=3,BC=CD=2,求DE与EF的长.