题目内容
如图,在正方形ABCD中,P为对角线BD上一点,PE⊥BC,垂足为E,PF⊥CD,垂足为F.求证:EF⊥AP.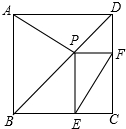

考点:正方形的性质
专题:证明题
分析:延长FP交AB交于G,延长AP交EF于点H,易证△PAG≌△EFP,可求得∠FPH+∠PFH=90°,可证得结论..
解答: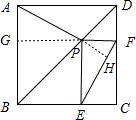 证明:如图,延长FP交AB于点G,延长AP交EF于点H,
证明:如图,延长FP交AB于点G,延长AP交EF于点H,
∵四边形ABCD为正方形,
∴∠C=∠ABC=90°,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF为矩形,
同理四边形BCFG也为矩形,
∴PE=FC=GB,
又∵BD平分∠ABC,
∴∠GBD=45°,
∴PG=BG=PE,
又∵AB=BC=CD,
∴AG=EC=PF,
在△PAG和△EFP中,
,
∴△PAG≌△EFP(SAS),
∴∠APG=∠FEP=∠FPH,
∵∠FEP+∠PFH=90°,
∴∠FPH+∠PFH=90°,
∴AP⊥EF.
 证明:如图,延长FP交AB于点G,延长AP交EF于点H,
证明:如图,延长FP交AB于点G,延长AP交EF于点H,∵四边形ABCD为正方形,
∴∠C=∠ABC=90°,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF为矩形,
同理四边形BCFG也为矩形,
∴PE=FC=GB,
又∵BD平分∠ABC,
∴∠GBD=45°,
∴PG=BG=PE,
又∵AB=BC=CD,
∴AG=EC=PF,
在△PAG和△EFP中,
|
∴△PAG≌△EFP(SAS),
∴∠APG=∠FEP=∠FPH,
∵∠FEP+∠PFH=90°,
∴∠FPH+∠PFH=90°,
∴AP⊥EF.
点评:本题主要考查正方形的性质及全等三角形的判定和性质,构造三角形全等找到角之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
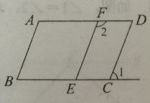 如图,∠2+∠D=180°,∠1=∠B,求证:AB∥EF.
如图,∠2+∠D=180°,∠1=∠B,求证:AB∥EF.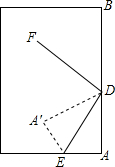 如图,斜折一页书的一角,使点A落在同一页书内的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE=
如图,斜折一页书的一角,使点A落在同一页书内的A′处,DE为折痕,作DF平分∠A′DB,试猜想∠FDE=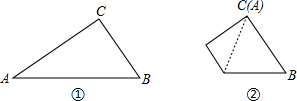 如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);
如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);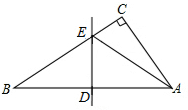 如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.AC=6,BC=8,∠CAE:∠BAE=1:2,
如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.AC=6,BC=8,∠CAE:∠BAE=1:2,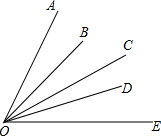 如图所示,五条射线OA、OB、OC、OD、OE组成的图形中共有几个角(小于90°)?如果从O点引出n条射线(最大角为锐角),能有多少个角(小于90°)?你能找出规律吗?
如图所示,五条射线OA、OB、OC、OD、OE组成的图形中共有几个角(小于90°)?如果从O点引出n条射线(最大角为锐角),能有多少个角(小于90°)?你能找出规律吗?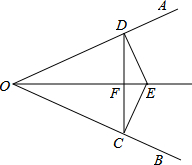 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F. 如图,已知矩形OABC的面积为25,它的对角线OB与双曲线
如图,已知矩形OABC的面积为25,它的对角线OB与双曲线