题目内容
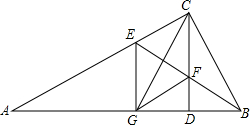 Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.
Rt△ABC中,CD是斜边AB上的高,BE平分∠CBA交AC于E,交CD于F,CG⊥BE交AB于G.(1)求证:四边形CFGE是菱形;
(2)若AG=4,BG=6,求AE和DF的长.
考点:菱形的判定与性质
专题:
分析:(1)先证明△BMG≌△BMC,得出MC=MG,再由线段垂直平分线性质证出EC=EG,FG=FC,然后证明EC=FC,即可证出结论;
(2)先求出BC=BG=6,再求出AC=8,然后证明△AEG∽△ABC,得出比例式
=
,求出AE=5,EC=CF=3,最后根据面积公式得到
AB•CD=
AC•BC,求出CD=
=4.8.即可得出DF=CD-CF.
(2)先求出BC=BG=6,再求出AC=8,然后证明△AEG∽△ABC,得出比例式
| AE |
| AB |
| AG |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BC |
| AB |
解答:解:(1)证明:设BE交CG于M.如图所示:
 ∵BE是∠CBA的平分线,
∵BE是∠CBA的平分线,
∴∠1=∠2,
∵CG⊥BE,
∴∠3=∠4=90°,
在△BMG和△BMC中,
,
∴△BMG≌△BMC(ASA),
∴MC=MG,
∴EC=EG,FG=FC,
∵CD⊥AB,
∴∠DFB+∠1=90°,
∵∠CEF+∠2=90°,∠CFE=∠DFB,
∴∠CEF=∠CFE,
∴EC=FC,
∴EC=EG=FG=FC,
∴四边形CFGE是菱形;
(2)根据题意得:△BEG≌△BEC,
∴BC=BG=6,∠BGE=∠BCA=90°,
∵AB=AG+BG=10,
∴AC=
=8,
∵∠A=∠A,∠ABG=∠BCA=90°,
∴△AEG∽△ABC,
∴
=
,即
=
,
∴AE=5.
∴EC=AC-AE=3,
∴CF=3,
∵
AB•CD=
AC•BC,
∴CD=
=
=4.8,
∴DF=CD-CF=4.8-3=1.8.
 ∵BE是∠CBA的平分线,
∵BE是∠CBA的平分线,∴∠1=∠2,
∵CG⊥BE,
∴∠3=∠4=90°,
在△BMG和△BMC中,
|
∴△BMG≌△BMC(ASA),
∴MC=MG,
∴EC=EG,FG=FC,
∵CD⊥AB,
∴∠DFB+∠1=90°,
∵∠CEF+∠2=90°,∠CFE=∠DFB,
∴∠CEF=∠CFE,
∴EC=FC,
∴EC=EG=FG=FC,
∴四边形CFGE是菱形;
(2)根据题意得:△BEG≌△BEC,
∴BC=BG=6,∠BGE=∠BCA=90°,
∵AB=AG+BG=10,
∴AC=
| 102-62 |
∵∠A=∠A,∠ABG=∠BCA=90°,
∴△AEG∽△ABC,
∴
| AE |
| AB |
| AG |
| AC |
| AE |
| 10 |
| 4 |
| 8 |
∴AE=5.
∴EC=AC-AE=3,
∴CF=3,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
| 8×6 |
| 10 |
∴DF=CD-CF=4.8-3=1.8.
点评:本题考查了菱形的判定、三角形全等的判定与性质以及勾股定理的运用等知识;培养学生综合运用定理进行推理和计算的能力.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 如图所示,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=7,DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为( )
如图所示,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=7,DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为( )A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
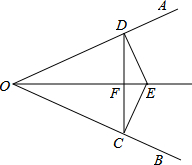 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F. 如图,已知矩形OABC的面积为25,它的对角线OB与双曲线
如图,已知矩形OABC的面积为25,它的对角线OB与双曲线 如图,六边形ABCDEF的每个内角都是120°,且AF=AB=3,BC=CD=2,求DE与EF的长.
如图,六边形ABCDEF的每个内角都是120°,且AF=AB=3,BC=CD=2,求DE与EF的长. 如图,在△ABC中,∠B=90°,AB=BC,D是BC上一点,且AB+BD=AD+DC.求证:∠BAD=30°.
如图,在△ABC中,∠B=90°,AB=BC,D是BC上一点,且AB+BD=AD+DC.求证:∠BAD=30°.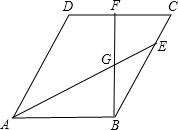 如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB
如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB 如图,将两个长方形叠在一起,得到四个正方形和一个长方形ABCD,已知四个正方形的面积和为60,长方形ABCD的周长为12,求长方形ABCD的面积.
如图,将两个长方形叠在一起,得到四个正方形和一个长方形ABCD,已知四个正方形的面积和为60,长方形ABCD的周长为12,求长方形ABCD的面积. 如图,在宽为20m,长为32m的长方形地面上修同样宽的两条不规则的路,余下的部分为耕地,若小路宽均为2m,求耕地面积为多少?
如图,在宽为20m,长为32m的长方形地面上修同样宽的两条不规则的路,余下的部分为耕地,若小路宽均为2m,求耕地面积为多少?