题目内容
18. 根据题意结合图形填空:
根据题意结合图形填空:(1)已知:如图1,DE∥BC,∠ADE=∠EFC,将说明∠1=∠2成立的理由填写完整.
解:∵DE∥BC (已知 )
∴∠ADE=∠ABC(两直线平行,同位角相等)
∵∠ADE=∠EFC(已知)
∴∠ABC=∠EFC∴DB∥EF(同位角相等,两直线平行)
∴∠1=∠2(两直线平行,内错角相等)
(2)已知:如图2,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
解:AD是∠BAC的平分线,
理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°(垂直定义)
∴AD∥EG(同位角相等,两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(两直线平行,内错角相等)
∵∠E=∠3(已知)
∴∠1=∠2
∴AD是∠BAC的平分线(角平分线定义).
分析 (1)根据平行线的性质得出∠ADE=∠ABC,求出∠ABC=∠EFC,根据平行线的判定得出DB∥EF,根据平行线的性质得出即可;
(2)根据平行线的判定得出AD∥EG,根据平行线的性质得出∠1=∠E,∠2=∠3,求出∠1=∠2,根据角平分线定义得出即可.
解答 解:(1)∵DE∥BC(已知)
∴∠ADE=∠ABC(两直线平行,同位角相等),
∵∠ADE=∠EFC (已知),
∴∠ABC=∠EFC,
∴DB∥EF(同位角相等,两直线平行),
∴∠1=∠2 (两直线平行,内错角相等),
故答案为:已知,∠ABC,两直线平行,同位角相等,(已知),∠ABC,∠EFC,(同位角相等,两直线平行),(两直线平行,内错角相等);
(2)解:AD是∠BAC的平分线,
理由如下:
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90° (垂直定义),
∴AD∥EG (同位角相等,两直线平行),
∴∠1=∠E (两直线平行,同位角相等),
∠2=∠3 (两直线平行,内错角相等),
∵∠E=∠3(已知)
∴∠1=∠2,
∴AD是∠BAC的平分线(角平分线定义),
故答案为:(垂直定义),(同位角相等,两直线平行),(两直线平行,同位角相等),(两直线平行,内错角相等),∠1,∠2,(角平分线定义).
点评 本题考查了角平分线定义和平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
8.已知关于x的一元二次方程x2+kx+k=0的一根是-2,则另一根x=( )
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
6.下列一元二次方程中没有实数根的是( )
| A. | (x-1)2=0 | B. | x2+3x+2=0 | C. | x2-4=0 | D. | x2+x+2=0 |
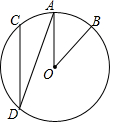 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是20°.
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是20°. 方程术是《九章算术》最高的数学成就,《九章算术》中“盈不足”一章中记载:“今有大器五小器一容三斛(古代的一种容量单位),大器一小器五容二斛,…”译文:“已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛,…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛.
方程术是《九章算术》最高的数学成就,《九章算术》中“盈不足”一章中记载:“今有大器五小器一容三斛(古代的一种容量单位),大器一小器五容二斛,…”译文:“已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛,…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛.