题目内容
8．已知关于x的一元二次方程x2+kx+k=0的一根是-2，则另一根x=（ ）| A． | -2 | B． | -4 | C． | 2 | D． | 4 |
分析 根据一元二次方程根与系数的关系列出方程，解方程即可．
解答 解：∵一元二次方程x2+kx+k=0的一根是-2，另一根是x，
∴-2+x=-k，-2x=k，
解得，x=-2，
故选：A．
点评 本题考查的是一元二次方程根与系数的关系，x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
百年学典课时学练测系列答案
相关题目
如图，⊙O是△ABC的外接圆，∠BOC=136°，则∠A的大小是68°．
16．如果关于x的方程（m+1）x2+2x-1=0有实数根，那么m的取值范围是（ ）
| A． | m≤-2 | B． | m≥-2且m≠-1 | C． | m≤-2且m≠-1 | D． | m≥-2 |
如图，等边三角形ABC内接于⊙O，点P是⊙O上一动点（点P不与点B，C重合），则∠CPB的度数为60°．
20．已知关于x的方程x2-2x-m=0有两个不相等的实数根，则m的取值范围为（ ）
| A． | m＜0 | B． | m＜-2 | C． | m≥0 | D． | m＞-1 |
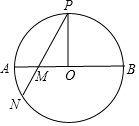如图，AB是⊙O的直径，PO⊥AB交⊙O于点P，弦PN与AB相交于点M，求证：PM•PN=2PO2．
根据题意结合图形填空：