题目内容
9．
如图，已知△ABC∽△ACP，∠A=70°，∠APC=65°，则∠B=45°．
分析 根据相似三角形对应角相等可得∠ACB=∠APC=65°，再根据三角形内角和定理即可求解．
解答 解：∵△ABC∽△ACP，
∴∠ACB=∠APC=65°，
∵∠A=70°，
∴∠B=180°-∠A-∠ACB=180°-70°-65°=45°．
故答案为45°．
点评 本题考查了相似三角形的性质，掌握相似三角形对应角相等是解题的关键．也考查了三角形内角和定理．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
20．
如图，AC垂直平分BD，垂足为E，连接AB，AD，BC，CD，下列结论不一定成立的是（ ）
如图，AC垂直平分BD，垂足为E，连接AB，AD，BC，CD，下列结论不一定成立的是（ ）| A． | AB=AD | B． | AC平分∠BCD | C． | AB=BD | D． | △BEC≌△DEC |
统计七年级若干名学生的跳高测试成绩，得到如图所示的频数分布直方图（每组数据含最小值，不含最大值）．请回答下列问题：
如图，△ABC和△DEF中，给出下列六个条件：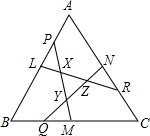
正△ABC，在边AB、BC、CA的正中间分别取点L、M、N，在边AL、BM、CN上分别取点P、Q、R，使LP=MQ=NR，当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时，使XY=XL，这时，△XYZ的面积是△ABC的几分之几？请写出思考过程．
18．关于反比例函数y=-$\frac{10}{x}$的图象，下列说法错误的是（ ）
| A． | 在第二，四象限 | B． | 和坐标轴都不相交 | ||
| C． | 绕着原点旋转180°后能与原图重合 | D． | 当x增大时，y一定减小 |
如图所示，△ABC内接于⊙O，sinB=$\frac{3}{5}$，AC=2cm，则⊙O的半径为多少厘米？