题目内容
4. 如图,△ABC和△DEF中,给出下列六个条件:
如图,△ABC和△DEF中,给出下列六个条件:①AB=DE;②BC=EF;③AC=DF;
④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F.
以其中三个条件为已知,能判断△ABC和△DEF全等的是①②③,①②⑤,①③④,②③⑥,①④⑤,②④⑤,③④⑤,②④⑤,②④⑥,②⑤⑥,③④⑤,③⑤⑥,③④⑥
(写出所有你认为正确的结论,写错一个该题得0分).
分析 根据全等三角形的判定方法分别进行组合即可.
解答 解:①②③可利用SSS定理判定△ABC和△DEF全等;
①②⑤可利用SAS定理判定△ABC和△DEF全等;
①③④可利用SAS定理判定△ABC和△DEF全等;
②③⑥可利用SAS定理判定△ABC和△DEF全等;
①④⑤可利用ASA定理判定△ABC和△DEF全等;
②④⑤可利用AAS定理判定△ABC和△DEF全等;
③④⑤可利用AAS定理判定△ABC和△DEF全等;
②④⑤可利用AAS定理判定△ABC和△DEF全等;
②④⑥可利用AAS定理判定△ABC和△DEF全等;
②⑤⑥可利用ASA定理判定△ABC和△DEF全等;
③④⑤可利用AAS定理判定△ABC和△DEF全等;
③⑤⑥可利用AAS定理判定△ABC和△DEF全等;
③④⑥可利用ASA定理判定△ABC和△DEF全等;
故答案为:①②③,①②⑤,①③④,②③⑥,①④⑤,②④⑤,③④⑤,②④⑤,②④⑥,②⑤⑥,③④⑤,③⑤⑥,③④⑥.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
14. 如图,直线a∥b,∠1=60°,那么∠2的度数是( )
如图,直线a∥b,∠1=60°,那么∠2的度数是( )
 如图,直线a∥b,∠1=60°,那么∠2的度数是( )
如图,直线a∥b,∠1=60°,那么∠2的度数是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
15.方程$\frac{2}{x-2}=\frac{1}{x}$的解是( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13. 如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )
如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )
 如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )
如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )| A. | 4 | B. | 6 | C. | 10 | D. | -10 |
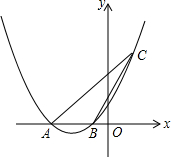 如图,二次函数y=$\frac{1}{4}$x2+($\frac{m}{4}$+1)x+m(其中m<4)的图象与x轴相交于A、B两点,且点A在点B的左侧.
如图,二次函数y=$\frac{1}{4}$x2+($\frac{m}{4}$+1)x+m(其中m<4)的图象与x轴相交于A、B两点,且点A在点B的左侧. 如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B=45°.
如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B=45°. 某运动器材的形状如图所示,以箭头所指的方向为左视方向,则它的俯视图是( )
某运动器材的形状如图所示,以箭头所指的方向为左视方向,则它的俯视图是( )


