题目内容
5. 如图,△ABC是边长为5的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为10.
如图,△ABC是边长为5的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为10.
分析 要求△AMN的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CND,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.
解答 解:∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°,
∵△ABC是边长为3的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
延长AB至F,使BF=CN,连接DF,
在△BDF和△CND中,
∵$\left\{\begin{array}{l}{BF=CN}\\{∠FBD=∠DCN}\\{DB=DC}\end{array}\right.$,
∴△BDF≌△CND(SAS),
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠BDM+∠BDF=60°,
在△DMN和△DMF中,
∵$\left\{\begin{array}{l}{MD=MD}\\{∠FDM=∠MDN}\\{DF=DN}\end{array}\right.$,
∴△DMN≌△DMF(SAS)
∴MN=MF,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=5+5=10.
点评 此题考查了全等三角形的判定与性质,等边三角形的性质;主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.

练习册系列答案
相关题目
16.甲、乙两名同学从学校出发到科技园去,甲每小时走4km,乙每小时走6km,甲出发1小时后,乙才出发,结果乙比甲早到20分钟,若设学校到科技园的距离为skm,则以下方程正确的是( )
| A. | $\frac{s}{4}+1=\frac{s}{6}$-20 | B. | $\frac{s}{4}+1=\frac{s}{6}-\frac{20}{60}$ | C. | $\frac{s}{4}-1=\frac{s}{6}-\frac{20}{60}$ | D. | $\frac{s}{4}-1=\frac{s}{6}+\frac{20}{60}$ |
10.小林在某商店购买商品A,B共三次,第一、两次均按标价购物,第三次购物时,商品A,B同时打6折,三次购物商品A,B的数量和费用如下表:
(1)求出商品A,B的标价;
(2)求第三次购物时的总费用是多少?
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 |
(2)求第三次购物时的总费用是多少?
 如图,⊙O是△ABC的外接圆,已知∠ABO=35°,则∠ACB=55度.
如图,⊙O是△ABC的外接圆,已知∠ABO=35°,则∠ACB=55度.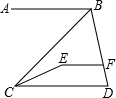 如图,已知AB∥CD,AB∥EF.
如图,已知AB∥CD,AB∥EF.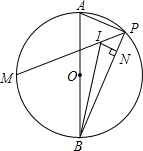 如图,AB为⊙O的直径,点M为半圆的中点,点P为另一半圆上一点(不与A、B重合),点I为△ABP的内心,IN⊥BP于N.
如图,AB为⊙O的直径,点M为半圆的中点,点P为另一半圆上一点(不与A、B重合),点I为△ABP的内心,IN⊥BP于N. 某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.
某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.