题目内容
6.计算(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12),运用哪种运算律可以避免通分( )| A. | 乘法分配律 | B. | 乘法结合律 | ||
| C. | 乘法交换律 | D. | 乘法结合律和交换律 |
分析 根据有理数的混合运算的运算方法,应用乘法分配律,求出(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12)的值是多少即可.
解答 解:计算(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12),运用乘法分配律可以避免通分.
(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12)
=1×(-12)-$\frac{1}{2}$×(-12)+$\frac{1}{3}$×(-12)+$\frac{1}{4}$×(-12)
=-12+6-4-3
=-13
故选:A.
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法分配律的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

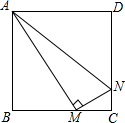 如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为$\frac{3}{8}$cm2.
如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为$\frac{3}{8}$cm2. 已知函数y=ax+b和y=kx+m的图象交于点A,则根据图象可知,关于x,y的二元一次方程组$\left\{{\begin{array}{l}{y=ax+b}\\{y=kx+m}\end{array}}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
已知函数y=ax+b和y=kx+m的图象交于点A,则根据图象可知,关于x,y的二元一次方程组$\left\{{\begin{array}{l}{y=ax+b}\\{y=kx+m}\end{array}}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$. 定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.
定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.