题目内容
1.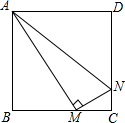 如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为$\frac{3}{8}$cm2.
如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为$\frac{3}{8}$cm2.
分析 设BM=xcm,则MC=(1-x)cm,当AM⊥MN时,利用互余关系可证△ABM∽△MCN,利用相似比求CN,根据三角形的面积公式表示出△ADN的面积,用二次函数的性质求面积的最小值.
解答 解:设BM=xcm,则MC=(1-x)cm,
∵∠AMN=90°,
∴∠AMB+∠NMC=90°,∠NMC+∠MNC=90°,
∴∠AMB=∠MNC,
又∵∠B=∠C,
∴△ABM∽△MCN,则$\frac{AB}{MC}$=$\frac{BM}{CN}$,即$\frac{1}{1-x}$=$\frac{x}{CN}$,
解得:CN=$\frac{x(1-x)}{1}$=x(1-x),
∴S△ADN=S正方形ABCD=$\frac{1}{2}$×1×[1-x(1-x)]=$\frac{1}{2}$x2-$\frac{1}{2}$x+$\frac{1}{2}$,
∵$\frac{1}{2}$<0,
∴当x=$\frac{1}{2}$cm时,S△ADN最小,最小值是$\frac{4×\frac{1}{2}×\frac{1}{2}-(-\frac{1}{2})^{2}}{4×\frac{1}{2}}$=$\frac{3}{8}$(cm2).
故答案是:$\frac{3}{8}$cm2.
点评 本题考查了二次函数的性质的运用.关键是根据已知条件判断相似三角形,利用相似比求函数关系式.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.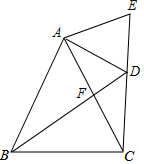 如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )
如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )
 如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )
如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.计算(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12),运用哪种运算律可以避免通分( )
| A. | 乘法分配律 | B. | 乘法结合律 | ||
| C. | 乘法交换律 | D. | 乘法结合律和交换律 |
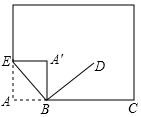 如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由.
如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由.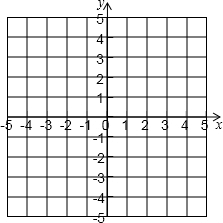 在平面直角坐标系中,将坐标是(0,4),(1,0),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
在平面直角坐标系中,将坐标是(0,4),(1,0),(3,0),(4,4)的点用线段依次连接起来形成一个图案. 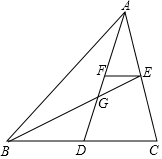 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么AF:AG=3:4.
如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么AF:AG=3:4.