题目内容
14.已知点A(4,-1)和点B(-2,2),以点A为圆心,AB长为半径作一个圆,则这个圆的直径长为6$\sqrt{5}$.分析 根据两点间的距离公式求得半径AB的长,继而可得圆的直径.
解答 解:∵AB=$\sqrt{(-2-4)^{2}+[2-(-1)]^{2}}$=3$\sqrt{5}$,
∴这个圆的直径长为2AB=6$\sqrt{5}$,
故答案为:6$\sqrt{5}$.
点评 本题主要考查两点间的距离公式和圆的基本性质,熟练掌握两点间的距离公式:两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
3.已知a,b,c分别是△ABC的三边,则$\sqrt{(a-b-c)^{2}}$-$\sqrt{(a+b-c)^{2}}$的值为( )
| A. | 2b | B. | -2b | C. | a+2c | D. | 2c-2a |
6.计算(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12),运用哪种运算律可以避免通分( )
| A. | 乘法分配律 | B. | 乘法结合律 | ||
| C. | 乘法交换律 | D. | 乘法结合律和交换律 |
 如图,点M、N是线段AB的勾股分割点(勾股分割点定义:指M、N把线段AB分割成AM,MN,和BN.若以AM,MN,和BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点).现若已知AM=3,MN=4,则BN=5或$\sqrt{7}$.
如图,点M、N是线段AB的勾股分割点(勾股分割点定义:指M、N把线段AB分割成AM,MN,和BN.若以AM,MN,和BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点).现若已知AM=3,MN=4,则BN=5或$\sqrt{7}$.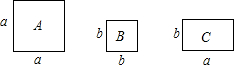 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?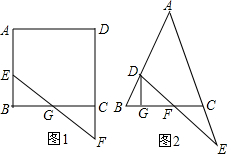 (1)如图1,E、F是正方形ABCD的边AB及DC延长线上的点,且BE=CF,则BG与BC的数量关系是BG=$\frac{1}{2}$BC.
(1)如图1,E、F是正方形ABCD的边AB及DC延长线上的点,且BE=CF,则BG与BC的数量关系是BG=$\frac{1}{2}$BC.