题目内容
11. 已知函数y=ax+b和y=kx+m的图象交于点A,则根据图象可知,关于x,y的二元一次方程组$\left\{{\begin{array}{l}{y=ax+b}\\{y=kx+m}\end{array}}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
已知函数y=ax+b和y=kx+m的图象交于点A,则根据图象可知,关于x,y的二元一次方程组$\left\{{\begin{array}{l}{y=ax+b}\\{y=kx+m}\end{array}}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
分析 点A(2,3)是两个函数图象的交点,同时满足函数解析式;即同时是函数解析式以及方程组的公共解,则关于x、y的二元一次方程组解即可求出.
解答 解:因为函数图象交点坐标为两函数解析式组成的方程组的解.
因此方程组$\left\{{\begin{array}{l}{y=ax+b}\\{y=kx+m}\end{array}}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
故答案为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程组的知识,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
6.计算(1-$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(-12),运用哪种运算律可以避免通分( )
| A. | 乘法分配律 | B. | 乘法结合律 | ||
| C. | 乘法交换律 | D. | 乘法结合律和交换律 |
16. 如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
 如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
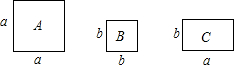 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?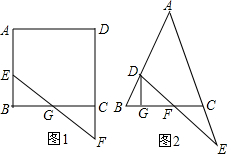 (1)如图1,E、F是正方形ABCD的边AB及DC延长线上的点,且BE=CF,则BG与BC的数量关系是BG=$\frac{1}{2}$BC.
(1)如图1,E、F是正方形ABCD的边AB及DC延长线上的点,且BE=CF,则BG与BC的数量关系是BG=$\frac{1}{2}$BC.