题目内容
18.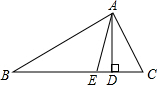 如图,AD是△ABC的高,AE是△ABC的角平分线,且∠BAC=90°,∠C=2∠B
如图,AD是△ABC的高,AE是△ABC的角平分线,且∠BAC=90°,∠C=2∠B求:(1)∠B的度数;
(2)∠DAE的度数.
分析 (1)根据直角三角形两锐角互余列出方程,再整理成关于∠B的方程,然后求解即可;
(2)根据直角三角形两锐角互余求出∠BAD,再求出∠BAE,然后根据∠DAE=∠BAD-∠BAE计算即可得解.
解答 解:(1)∵∠BAC=90°,
∴∠B+∠C=90°,
∵∠C=2∠B,
∴∠B+2∠B=90°,
解得∠B=30°;
(2)∵AD是△ABC的高,
∴∠BAD=90°-∠B=90°-30°=60°,
∵AE是△ABC的角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×90°=45°,
∴∠DAE=∠BAD-∠BAE=60°-45°=15°.
点评 本题考查了三角形的内角和定理,角平分线的定义,利用直角三角形两锐角互余列方程更简便.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
4.已知关于x,y的方程组$\left\{\begin{array}{l}{x+2y=7m}\\{2x-y=4m}\end{array}\right.$的解为3x+2y=13的一个解,那么m的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
7.某校组织初三学生电脑技能竞赛,每班选派相同人数去参加竞赛,竞赛成绩分A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.将初三(1)班和(2)班的成绩整理并绘制成统计图如下.

(1)此次竞赛中(2)班成绩在C级以上(包括C级)的人数为17;
(2)请你将表格补充完整:
(3)试运用所学的统计知识,从两个不同角度评价初三(1)班和初三(2)班的成绩.

(1)此次竞赛中(2)班成绩在C级以上(包括C级)的人数为17;
(2)请你将表格补充完整:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 1班 | 87.5 | 90 | ②90 |
| 2班 | 88 | ①85 | 100 |
 如图,在△ABC中,∠C=90°,AE平分∠BAC,CE=3,AB=8,则△ABE的面积等于12.
如图,在△ABC中,∠C=90°,AE平分∠BAC,CE=3,AB=8,则△ABE的面积等于12.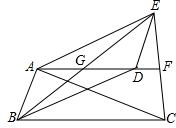 已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC.
已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC. 如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点0.
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点0.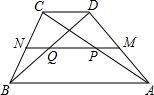 梯形ADCB中,AB∥CD,中位线MN与对角线AC,BD分别交于P,Q,设梯形ADCB的周长为L,四边形PDCQ的周长为L1,若AB=2CD,求L1:L的值.
梯形ADCB中,AB∥CD,中位线MN与对角线AC,BD分别交于P,Q,设梯形ADCB的周长为L,四边形PDCQ的周长为L1,若AB=2CD,求L1:L的值.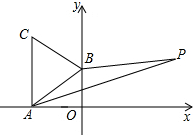 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.