题目内容
6.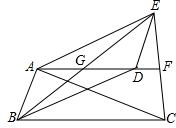 已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC.
已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC.
分析 由AB∥DE,BD∥AE,得到四边形ABDE是平行四边形,根据平行四边形的性质得到EG=GB,EG=$\frac{1}{2}$EB,由等腰三角形的性质得到EF=FC,EF=$\frac{1}{2}$EC,推出△GEF∽△BEC,得到∠EGF=∠EBC,根据平行线的判定即可得到结论.
解答 解:∵AB∥DE,BD∥AE,
∴四边形ABDE是平行四边形,
∴EG=GB,EG=$\frac{1}{2}$EB,
∵在△ACE中,AC=AE,AF⊥CE,
∴EF=FC,EF=$\frac{1}{2}$EC,
∵∠GEF=∠BEC,$\frac{EG}{EB}$=$\frac{EF}{EC}$=$\frac{1}{2}$,
∴△GEF∽△BEC,
∴∠EGF=∠EBC,
∴FG∥BC.
点评 本题考查了平行四边形的判定和性质,相似三角形的判定和性质,等腰三角形的性质,平行线的判定,熟练掌握平行四边形的判定和性质是解题的关键.

练习册系列答案
相关题目
15.一元二次方程x2-4x+1=0的两根是x1,x2,则x1•x2的值是( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
 -2和2对应的点将数轴分成3段,如果数轴上任意n个不同的点中至少有3个在其中之ㄧ段,那么n的最小值是( )
-2和2对应的点将数轴分成3段,如果数轴上任意n个不同的点中至少有3个在其中之ㄧ段,那么n的最小值是( )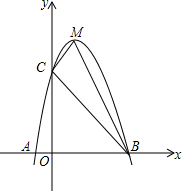 如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).
如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).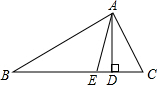 如图,AD是△ABC的高,AE是△ABC的角平分线,且∠BAC=90°,∠C=2∠B
如图,AD是△ABC的高,AE是△ABC的角平分线,且∠BAC=90°,∠C=2∠B