题目内容
10.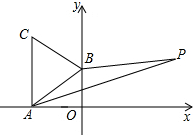 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.
分析 过P点作PD⊥x轴,垂足为D,根据A(-$\sqrt{3}$,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用S△ABP=S△AOB+S梯形BODP-S△ADP,列方程求a.
解答 解:过P点作PD⊥x轴,垂足为D.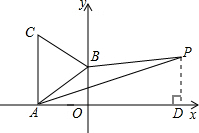
由A(-$\sqrt{3}$,0)、B(0,1),得OA=$\sqrt{3}$,OB=1,
∵△ABC为等边三角形,
由勾股定理,得AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2,
∴S△ABC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
又∵S△ABP=S△AOB+S梯形BODP-S△ADP
=$\frac{1}{2}$×$\sqrt{3}$×1+$\frac{1}{2}$×(1+a)×3-$\frac{1}{2}$×($\sqrt{3}$+3)×a
=$\frac{\sqrt{3}+3-\sqrt{3}a}{2}$,
由2S△ABP=S△ABC,得$\sqrt{3}+3-\sqrt{3}a$=$\sqrt{3}$,
∴a=$\sqrt{3}$.
点评 本题考查了点的坐标与线段长的关系,根据图形间的面积关系列出关于a的方程是解题的关键.

练习册系列答案
相关题目
15.一元二次方程x2-4x+1=0的两根是x1,x2,则x1•x2的值是( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
 -2和2对应的点将数轴分成3段,如果数轴上任意n个不同的点中至少有3个在其中之ㄧ段,那么n的最小值是( )
-2和2对应的点将数轴分成3段,如果数轴上任意n个不同的点中至少有3个在其中之ㄧ段,那么n的最小值是( ) 如图,AD是△ABC的高,AE是△ABC的角平分线,且∠BAC=90°,∠C=2∠B
如图,AD是△ABC的高,AE是△ABC的角平分线,且∠BAC=90°,∠C=2∠B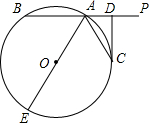 如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D.
如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为D. 如图所示圆中,AB为直径,弦CD⊥AB,垂足为H.若HB=2,HD=4,则AH=8.
如图所示圆中,AB为直径,弦CD⊥AB,垂足为H.若HB=2,HD=4,则AH=8.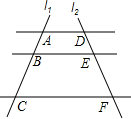 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于A,B,C和点D,E,F.若AB=2,BC=4,DE=3,则EF的长为( )
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于A,B,C和点D,E,F.若AB=2,BC=4,DE=3,则EF的长为( )