题目内容
18.从-3,-2,-1,0,1,3,4这七个数中随机抽取一个数记为a,a的值既是不等式组$\left\{\begin{array}{l}{2x+3<4}\\{3x-1>-11}\end{array}\right.$的解,又在函数y=$\frac{1}{2{x}^{2}+2x}$的自变量取值范围内的概率是$\frac{2}{7}$.分析 由a的值既是不等式组 $\left\{\begin{array}{l}{2x+3<4}\\{3x-1>-11}\end{array}\right.$的解,又在函数y=$\frac{1}{2{x}^{2}+2x}$的自变量取值范围内的有-3,-2,可直接利用概率公式求解即可求得答案.
解答 解:∵不等式组 $\left\{\begin{array}{l}{2x+3<4}\\{3x-1>-11}\end{array}\right.$的解集是:-$\frac{10}{3}$<x<$\frac{1}{2}$,
∴a的值既是不等式组 $\left\{\begin{array}{l}{2x+3<4}\\{3x-1>-11}\end{array}\right.$的解的有:-3,-2,-1,0,
∵函数y=$\frac{1}{2{x}^{2}+2x}$的自变量取值范围为:2x2+2x≠0,
∴在函数y=$\frac{1}{2{x}^{2}+2x}$的自变量取值范围内的有-3,-2,4;
∴a的值既是不等式组$\left\{\begin{array}{l}{2x+3<4}\\{3x-1>-11}\end{array}\right.$的解,又在函数y=$\frac{1}{2{x}^{2}+2x}$的自变量取值范围内的有:-3,-2;
∴a的值既是不等式组$\left\{\begin{array}{l}{2x+3<4}\\{3x-1>-11}\end{array}\right.$的解,又在函数y=$\frac{1}{2{x}^{2}+2x}$的自变量取值范围内概率是:$\frac{2}{7}$.
故答案为:$\frac{2}{7}$
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比,解此题需要求出不等式组的解集和函数自变量的取值范围.

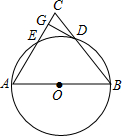 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.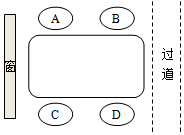 莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
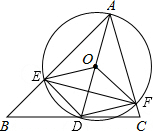 如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.
如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.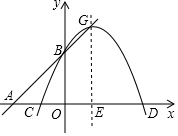 已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中
已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中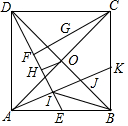 如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )
如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )