题目内容
3.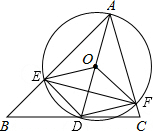 如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.
如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.(1)求$\frac{EF}{OE}$的值;
(2)当AD运动到什么位置时,四边形OEDF正好是菱形,请说明理由.
(3)点D运动过程中,线段EF的最小值为5$\sqrt{3}$(直接写出结果).
分析 (1)根据已知条件即可得到结论;
(2)根据角平分线的性质得到DE=DF,有AD是⊙O的直径,得到∠DEA=90°,由三角形的内角和得到∠EDA=60°,推出△OED是等边三角形,得到ED=OE,根据菱形的判定定理即可得到结论;
(3)由垂线的性质可知,当AD⊥BC时,直径AD最短,即⊙O最小,即EF由最小值,连接OE,OF,过O作OH⊥EF于H,解直角三角形即可得到结论.
解答 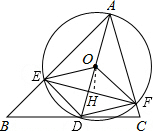 解:(1)∵∠BAC=60°,
解:(1)∵∠BAC=60°,
∴∠EOF=120°,
∵OE=OF,
∴$\frac{EF}{OE}$=$\sqrt{3}$;
(2)当AD平分∠BAC时,四边形OEDF是菱形,
理由:∵AD平分∠BAC,
∴DE=DF,∠BAD=30°,
∵AD是⊙O的直径,
∴∠DEA=90°,
∴∠EDA=60°,
∵OE=OD,
∴△OED是等边三角形,即ED=OE,
∴OE=OF=DE=DF,
∴四边形OEDF是菱形;
(3)由垂线的性质可知,
当AD⊥BC时,直径AD最短,即⊙O最小,即EF有最小值,
如图,过O作OH⊥EF于H,
在Rt△ADB中,
∵∠ABC=45°,AB=10$\sqrt{2}$,
∴AD=BD=10,
即此时,⊙O的直径为10,
∵∠EOH=$\frac{1}{2}$∠EOH=∠BAC=60°,
∴EH=OE•sin∠EOH=5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$,
由垂径定理可得EF=2EH=5$\sqrt{3}$.
线段EF的最小值为5$\sqrt{3}$,
故答案为:5$\sqrt{3}$.
点评 本题考查了菱形的判定,垂径定理,圆周角定理,解直角三角形,关键是根据运动变化,找出满足条件的最小圆.

练习册系列答案
相关题目
13.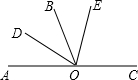 如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )
如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )
 如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )
如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )| A. | 36° | B. | 72° | C. | 44° | D. | 56° |
11.我市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容,规定:每一位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.小刚抽到物理实验B和化学实验F的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
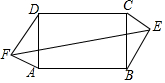 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于$\sqrt{394}$.
如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于$\sqrt{394}$.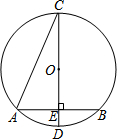 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为4cm.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为4cm.