题目内容
8.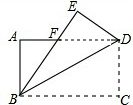 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{5}{13}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{7}$ |
分析 由矩形ABCD中,沿对角线BD折叠,得△BED,易得△BFD是等腰三角形,然后设AB=2x,AF=a,则AD=3x,由勾股定理即可求得(2x)2+a2=(3x-a)2,继而求得答案.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,
∴∠BDF=∠CBD,
由折叠的性质:∠DBF=∠CBD,
∴∠BDF=∠DBF,
∴BF=DF,
∵矩形ABCD中,3AB=2AD,
∴设AB=2x,AF=a,则AD=3x,
∴DF=AD-AF=3x-a,
∴BF=DF=3x-a,
在Rt△ABF中,AB2+AF2=BF2,
∴(2x)2+a2=(3x-a)2,
解得:a=$\frac{5}{6}$x,
∴AF=$\frac{5}{6}$x,DF=$\frac{13}{6}$x,
∴$\frac{AF}{FD}$=$\frac{5}{13}$.
故选B.
点评 此题考查了折叠的性质、矩形的性质以及勾股定理.注意掌握折叠前后图形的对应关系是解此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13.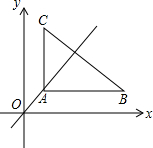 如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
 如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )| A. | 5 | B. | $\frac{25}{4}$ | C. | 9 | D. | 16 |
16.将四个编号为1,2,3,4的小球随机放入4个编号为1,2,3,4的盒子中.记f(i)为第i个盒子中小球的编号与盒子编号的差的绝对值.则f(1)+f(2)+f(3)+f(4)=4的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{5}{24}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{24}$ |
18.已知b<0,则二次根式-$\sqrt{{a}^{3}b}$的化简结果是( )
| A. | -a$\sqrt{-ab}$ | B. | -a$\sqrt{ab}$ | C. | a$\sqrt{ab}$ | D. | a$\sqrt{-ab}$ |
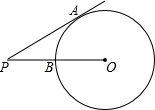 如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.
如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.