题目内容
13.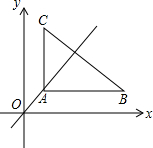 如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )| A. | 5 | B. | $\frac{25}{4}$ | C. | 9 | D. | 16 |
分析 根据等腰直角三角形和y=x的特点,求出BC的中点坐标,即可求解.
解答 解:根据题意可知点A的坐标为(1,1).
∵∠BAC=90°,AB=AC=4,
∴点B,C关于直线y=x对称,
∴点B的坐标为(5,1),点C的坐标为(1,5),
∴线段BC中点的横坐标为$\frac{5+1}{2}$=3,纵坐标为$\frac{1+5}{2}$=3,
∴线段BC的中点坐标为(3,3),
∵双曲线y=$\frac{k}{x}$与等腰三角形ABC有公共点,
∴k的最大值为过B,C中点的双曲线,此时k=9.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,等腰直角三角形的性质.注意直线,三角形的特殊性,根据双曲线上点的坐标特点求解.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
3.下列各式中能用平方差公式计算的是( )
| A. | (a+3b)(3a-b) | B. | (3a-b)(3a-b) | C. | (3a-b)(-3a+b) | D. | (3a-b)(3a+b) |
4.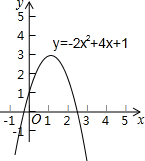 在求解一元二次方程-2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=-2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出-1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )
在求解一元二次方程-2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=-2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出-1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )
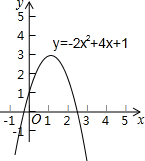 在求解一元二次方程-2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=-2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出-1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )
在求解一元二次方程-2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=-2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出-1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )| A. | 类比 | B. | 演绎 | C. | 数形结合 | D. | 公理化 |
18.已知∠1=42°45′,则∠1的余角等于( )
| A. | 47°55′ | B. | 47°15′ | C. | 48°15′ | D. | 137°55′ |
8.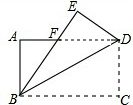 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{5}{13}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{7}$ |
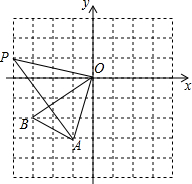 如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.
如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.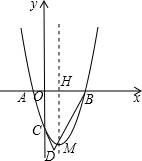 如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.
如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.