题目内容
11.下列是三元一次方程组$\left\{\begin{array}{l}{x+2y+z=16}\\{2x=3y=6z}\end{array}\right.$的解的是( )| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\\{z=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=6}\\{y=3}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6}\\{y=4}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=5}\\{z=6}\end{array}\right.$ |
分析 方程组整理后,利用代入消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{x+2y+z=16①}\\{2x=3y②}\\{3y=6z③}\end{array}\right.$,
由②得:x=$\frac{3}{2}$y,由③得:z=$\frac{1}{2}$y,
代入①得:$\frac{3}{2}$y+2y+$\frac{1}{2}$y=16,即y=4,
把y=4代入得:x=6,z=2,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=4}\\{z=2}\end{array}\right.$.
故选C.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
16. 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | (a+b)(a-b)=a2-b2 | D. | a(a-b)=a2-ab |
 如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)
如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)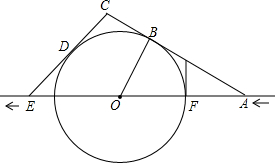 如图,某船在大海中沿航线由东向西行驶,行驶到A时,发现前方20海里的F处出现暗礁,经进一步观察发现前方以点O为圆心(点O在航线上),OF长为半径的区域内充满暗礁,该船马上改变航向,从点A沿北偏西60°方向前进,与⊙O切于点B后到达点C,接着,该船从点C沿南偏西45°方向前进,与⊙O切于点D后回到航线上点E,然后继续沿原航线行驶,请解决下列问题:暗礁区域的半径为多少海里?
如图,某船在大海中沿航线由东向西行驶,行驶到A时,发现前方20海里的F处出现暗礁,经进一步观察发现前方以点O为圆心(点O在航线上),OF长为半径的区域内充满暗礁,该船马上改变航向,从点A沿北偏西60°方向前进,与⊙O切于点B后到达点C,接着,该船从点C沿南偏西45°方向前进,与⊙O切于点D后回到航线上点E,然后继续沿原航线行驶,请解决下列问题:暗礁区域的半径为多少海里?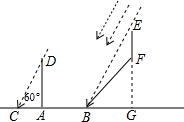 如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°
如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°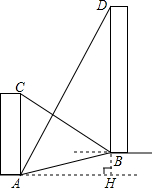 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)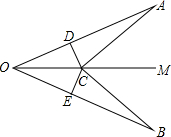 已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.
已知:如图,OM是∠AOB的平分线,C是OM上一点,且CD⊥OA于D,CE⊥OB于E,AD=EB.求证:AC=CB.
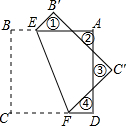 如图,正方形纸片ABCD的边长为4,将其沿EF折叠,则图中①②③④四个三角形的周长之和为16.
如图,正方形纸片ABCD的边长为4,将其沿EF折叠,则图中①②③④四个三角形的周长之和为16.