题目内容
19.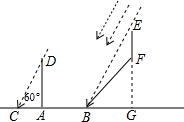 如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°
如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°(1)若小丽正站在水平地面A处上时,那么她的影长为多少米?
(2)若小丽来到一个坡度i=1:1的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上.
分析 (1)在Rt△ACD中,利用正切的定义求解;
(2)先根据坡度的定义得到BG=GF,设BG=x,则FG=x,由于小芳的影子恰好都落在坡面上,则∠EBG=60°,在Rt△EBG中利用正切定义计算出x=$\frac{4(\sqrt{3}+1)}{5}$,然后根据等腰直角三角形的性质得到BF=$\sqrt{2}$x=$\frac{4(\sqrt{6}+\sqrt{2})}{5}$.
解答 解:(1)在Rt△ACD中,AD=1.6,∠ACD=60°,
∵tan∠ACD=$\frac{AD}{AC}$,
∴AC=$\frac{1.6}{tan60°}$=$\frac{1.6}{\sqrt{3}}$=$\frac{8\sqrt{3}}{15}$,
即她的影长为$\frac{8\sqrt{3}}{15}$米;
(2)如图,∵i=1:1,
∴BG=GF,
设BG=x,则FG=x,
∵小芳的影子恰好都落在坡面上,
∴∠EBG=60°,
在Rt△EBG中,∵tan∠EBG=$\frac{EG}{BG}$,
∴(1.6+x)=$\sqrt{3}$x,解得x=$\frac{4(\sqrt{3}+1)}{5}$,
∴BF=$\sqrt{2}$x=$\frac{4(\sqrt{6}+\sqrt{2})}{5}$,
即她在坡面上至少前进$\frac{4(\sqrt{6}+\sqrt{2})}{5}$米时,小芳的影子恰好都落在坡面上.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.也考查了坡度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列是三元一次方程组$\left\{\begin{array}{l}{x+2y+z=16}\\{2x=3y=6z}\end{array}\right.$的解的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\\{z=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=6}\\{y=3}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6}\\{y=4}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=5}\\{z=6}\end{array}\right.$ |
8.中新网2014年11月19日电 据财政部网站消息,为保证城乡义务教育阶段学校春季开学后正常运转和“两免一补”政策落实到位,中央财政下达2015年城乡义务教育补助经费部分预算697.2亿元.将697.2亿用科学记数法表示应为( )
| A. | 6.972×1011 | B. | 6.972×1010 | C. | 0.6972×103 | D. | 6.972×102 |
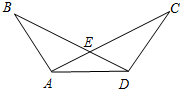 已知:如图,AC、BD相交于点E,AB=DC,∠B=∠C.求证:∠EAD=∠EDA.
已知:如图,AC、BD相交于点E,AB=DC,∠B=∠C.求证:∠EAD=∠EDA.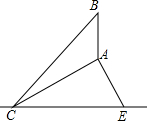 如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?
如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?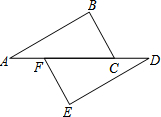 如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.