题目内容
20. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).
分析 根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号,从而判断①;根据对称轴得到函数图象经过(3,0),则得②的判断;根据图象经过(-1,0)可得到a、b、c之间的关系,从而对②⑤作判断;利用$\frac{4ac{-b}^{2}}{4a}<-1$,可判断③;从图象与y轴的交点B在(0,-2)和(0,-1)之间可以判断c的大小得出④的正误.
解答 解:①∵函数开口方向向上,
∴a>0;
∵对称轴在y轴右侧
∴ab异号,
∵抛物线与y轴交点在y轴负半轴,
∴c<0,
∴abc>0,
故①正确;
②∵图象与x轴交于点A(-1,0),对称轴为直线x=1,
∴图象与x轴的另一个交点为(3,0),
∴当x=2时,y<0,
∴4a+2b+c<0,
故②错误;
③∵二次函数y=ax2+bx+c的图象与y轴的交点在(0,-1)的下方,对称轴在y轴右侧,a>0,
∴最小值:$\frac{4ac{-b}^{2}}{4a}$<-1,
∵a>0,
∴4ac-b2<-4a;
∴③正确;
④∵图象与y轴的交点B在(0,-2)和(0,-1)之间,
∴-2<c<-1
∴-2<-3a<-1,
∴$\frac{2}{3}$>a>$\frac{1}{3}$;
故④正确
⑤∵a>0,
∴b-c>0,即b>c;
故⑤正确.
综上所述,正确的有①③④⑤,
故答案为:①③④⑤.
点评 此题主要考查图象与二次函数系数之间的关系.解题关键是注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.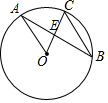 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
12. 如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
 如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )| A. | 20 | B. | 19 | C. | 18 | D. | 16 |
9.已知a<b,则下列式子中成立的是( )
| A. | a+3>b+3 | B. | 3-a>3-b | C. | a-3>b-3 | D. | -3a<-3b |

 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=180度.
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=180度.