题目内容
12. 如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )| A. | 20 | B. | 19 | C. | 18 | D. | 16 |
分析 延长AO交BC于D,根据∠A、∠B的度数易证得△ABD是等边三角形,由此可求出OD、BD的长;过O作BC的垂线,设垂足为E;在Rt△ODE中,根据OD的长及∠ODE的度数易求得DE的长,进而可求出BE的长;由垂径定理知BC=2BE,由此得解.
解答 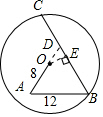 解:延长AO交BC于D,作OE⊥BC于E;
解:延长AO交BC于D,作OE⊥BC于E;
∵∠A=∠B=60°,∴∠ADB=60°;
∴△ADB为等边三角形;
∴BD=AD=AB=12;
∴OD=4,又∵∠ADB=60°,
∴DE=$\frac{1}{2}$OD=2;
∴BE=10;
∴BC=2BE=20.
故选A.
点评 此题主要考查了等边三角形的判定和性质以及垂径定理的应用,正确作出辅助线是关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
17.三角形三边分别是下列各组数,能组成直角三角形的是( )
| A. | 2,3,4 | B. | 2,3,5 | C. | 6,8,9 | D. | 6,8,10 |
4.下列方程中的解不是x=$\frac{1}{3}$的方程是( )
| A. | 6x-1=1 | B. | 7x-1=x+1 | C. | 2x=$\frac{2}{3}$ | D. | 5x-x=2 |
2.已知点M(1,a)和点N(2,b)是一次函数y=-2x+n图象上的两点,则a与b的大小关系是( )
| A. | a≤b | B. | a<b | C. | a≥b | D. | a>b |
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号). 如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.有下列结论:①MN=$\frac{4\sqrt{3}}{3}$;②若MN与⊙O相切,则AM=$\sqrt{3}$;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.有下列结论:①MN=$\frac{4\sqrt{3}}{3}$;②若MN与⊙O相切,则AM=$\sqrt{3}$;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )