题目内容
8.一位汽车司机准备去商场购物,然后他随意把汽车停在某个停车场内,停车场分A、B两区,停车场内一个停车位置正好占一个方格且每一个方格除颜色外完全一样,则汽车停在B区阴影区域的概率是$\frac{5}{9}$.
分析 根据几何概率的求法,在B区,用蓝色区域的面积除以B区的总面积可得到汽车停在B区蓝色区域的概率.
解答 解:B区域内,共等分为9部分,阴影区域为5部分,
所以汽车停在B区阴影区域的概率是$\frac{5}{9}$,
故答案为:$\frac{5}{9}$.
点评 本题考查了几何概率:求概率时,已知和未知与几何有关的就是几何概率.计算方法是长度比,面积比,体积比等.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
18.实验中学团委举办了“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上获优胜奖,达到9分以上获优秀奖.这次竞赛中初中、高中两组学生成绩分布的条形统计图如下:
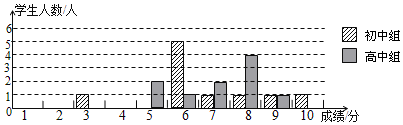
(1)补充完成下列的成绩统计分析表:
(2)安欣同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知:安欣是初中组学生(填“初中”或“高中”);
(3)初中组同学说他们组的优胜奖率、优秀奖率均高于高中组,所以他们组的成绩好于高中组.但高中组同学不同意初中组同学的说法,认为他们组的成绩要好于初中组.请你给出两条支持高中组同学观点的理由.

(1)补充完成下列的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 众数 | 方差 | 优胜奖率 | 优秀奖率 |
| 初中 | 6.7 | 6 | 6 | 3.41 | 90% | 20% |
| 高中 | 7.1 | 7.5 | 8 | 1.69 | 80% | 10% |
(3)初中组同学说他们组的优胜奖率、优秀奖率均高于高中组,所以他们组的成绩好于高中组.但高中组同学不同意初中组同学的说法,认为他们组的成绩要好于初中组.请你给出两条支持高中组同学观点的理由.
19.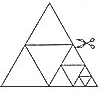 如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
 如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )| A. | 3n-1 | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
13.已知代数式2x+y的值是3,则代数式8x+4y+1的值是( )
| A. | 1 | B. | 4 | C. | 13 | D. | 不能确定 |
17.三角形三边分别是下列各组数,能组成直角三角形的是( )
| A. | 2,3,4 | B. | 2,3,5 | C. | 6,8,9 | D. | 6,8,10 |
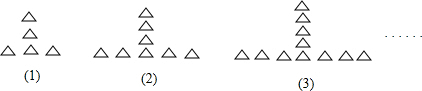
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).