题目内容
5. 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=180度.
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=180度.
分析 先利用∠AOD+∠COD=90°,∠COD+∠BOC=90°,可得∠AOD+∠COD+∠COD+∠BOC=180°,而∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,于是有∠AOB+∠COD=180°.
解答 解:∵∠AOD+∠COD=90°,∠COD+∠BOC=90°,
∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,
∴∠AOD+∠COD+∠COD+∠BOC=180°,
∴∠AOD+2∠COD+∠BOC=180°,
∴∠AOB+∠COD=180°.
故答案为:180
点评 本题考查了余角的概念,掌握同角的余角相等这一性质;能够根据图形正确表示角之间的和的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )| A. | △ABC三边的垂直平分线的交点 | B. | △ABC的三条中线的交点 | ||
| C. | △ABC三条角平分线的交点 | D. | △ABC三条高所在直线的交点 |
13.已知代数式2x+y的值是3,则代数式8x+4y+1的值是( )
| A. | 1 | B. | 4 | C. | 13 | D. | 不能确定 |
17.三角形三边分别是下列各组数,能组成直角三角形的是( )
| A. | 2,3,4 | B. | 2,3,5 | C. | 6,8,9 | D. | 6,8,10 |
15.在一个口袋中有5个除颜色外完全相同的小球,其中有3个黄球,1个黑球,1个白球,从中随机摸出一个小球,则摸到黄球的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).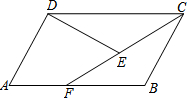 在平行四边形ABCD中,点F为边AB上一点,且CD=CF,AF=EF,连结D、E.求证:DE=BC.
在平行四边形ABCD中,点F为边AB上一点,且CD=CF,AF=EF,连结D、E.求证:DE=BC.