题目内容
13.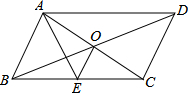 如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )
如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=$\frac{1}{2}$BC,得到AE=$\frac{1}{2}$BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S?ABCD=AB•AC,故②正确,根据AB=$\frac{1}{2}$BC,OB=$\frac{1}{2}$BD,且BD>BC,得到AB≠OB,故③错误;根据题意得出故④不正确;即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=$\frac{1}{2}$BC,
∴AE=$\frac{1}{2}$BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB•AC,故②正确,
∵AB=$\frac{1}{2}$BC,OB=$\frac{1}{2}$BD,
∵BD>BC,
∴AB≠OB,故③错误;④不正确;
∵若∠COD=60°,
则∠ADO=60°-30°=30°=∠CAD,
∴OA=OD,
∴AC=BD,矛盾,
故④不正确.
故选:B.
点评 本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式,熟练掌握性质定理和判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.△ABC的三边长分别是1、k、3,则化简$7-\sqrt{4{k^2}-36k+81}-|{2k-3}|$的结果为( )
| A. | -5 | B. | 19-4k | C. | 13 | D. | 1 |
 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOD=20°,求∠COE的度数.
如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOD=20°,求∠COE的度数.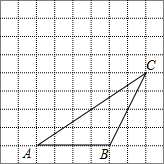 如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′、中线A′E.
如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′、中线A′E.
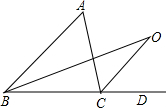 已知,在△ABC中,∠ABC和∠ACD的平分线相交于点O,
已知,在△ABC中,∠ABC和∠ACD的平分线相交于点O,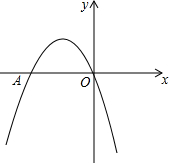 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).