题目内容
3.(1)计算:$({\sqrt{\frac{3}{8}}-2\sqrt{3}})×\sqrt{6}+\sqrt{72}$(2)解方程:9(3x+1)2=4(x-1)2.
分析 (1)根据运算法则进行计算即可;
(2)应用因式分解法即可解得.
解答 解:(1)$({\sqrt{\frac{3}{8}}-2\sqrt{3}})×\sqrt{6}+\sqrt{72}$
=$\frac{3}{2}$-6$\sqrt{2}$+6$\sqrt{2}$
=$\frac{3}{2}$;
(2)9(3x+1)2=4(x-1)2.
[3(3x+1)+2(x-1)][3(3x+1)-2(x-1)]=0,
(11x+1)(7x+5)=0,
∴11x+1=0,7x+5=0,
∴${x_1}=-\frac{5}{7},{x_2}=-\frac{1}{11}$.
点评 本题考查了二次根式的混合运算和因式分解法解一元二次方程,熟练掌握运算法则和解方程的方法是解题的关键.

练习册系列答案
相关题目
13.已知$\sqrt{{(1-2x)}^2}=2x-1$,则x的取值范围是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x<$\frac{1}{2}$ |
14.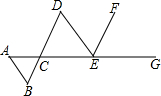 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )| A. | 0个 | B. | 1个 | C. | 3个 | D. | 5个 |
15.下列运算正确的是( )
| A. | a3•a4=a12 | B. | a3÷a3=0 | C. | a3+a3=2a6 | D. | 3a2•5a3=15a5 |
12.若∠α+∠β=180°,∠β+∠γ=180°,则∠α与∠γ的关系是( )
| A. | 互余 | B. | 互补 | C. | 相等 | D. | ∠α=90°+∠γ |
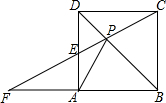 如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.
如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.