题目内容
14.下面四个二次函数解析式中,开口方向不同的那个是( )| A. | y=2x2-3x+1 | B. | y=(x-5)(x-6) | C. | $y=\frac{1}{2}{({x+1})^2}-3$ | D. | y=x-x2-4 |
分析 根据二次项的系数的符号确定开口方向即可.
解答 解:A、a=2>0,开口向上;
B、a=1>0,开口向上;
C、a=${\frac{1}{2}}_{\;}$>0,开口向上;
D、a=-1<0,开口向下;
故选D.
点评 考查了二次函数的性质,解题的关键是了解二次函数的开口方向取决于二次项的系数,难度不大.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
2.下列命题是假命题的是( )
| A. | 同弧或等弧所对的圆周角相等 | B. | 平分弦的直径垂直于弦 | ||
| C. | 两条平行线间的距离处处相等 | D. | 直径所对的圆周角等于90° |
19.一根1米长的小棒,第一次截去它的$\frac{1}{3}$,第二次截去剩下的$\frac{1}{3}$,如此截下去,第五次后剩下的小棒的长度是( )
| A. | ${({\frac{1}{3}})^5}$米 | B. | ${({\frac{2}{3}})^5}$米 | C. | $[{1-{{({\frac{1}{3}})}^5}}]$米 | D. | $[{1-{{({\frac{2}{3}})}^5}}]$米 |
6. 如图,用火柴棍拼成一排由三角形组成的图形,按此规律,如果图形中含有41根火柴棍,则可以拼成的三角形的个数为( )
如图,用火柴棍拼成一排由三角形组成的图形,按此规律,如果图形中含有41根火柴棍,则可以拼成的三角形的个数为( )
 如图,用火柴棍拼成一排由三角形组成的图形,按此规律,如果图形中含有41根火柴棍,则可以拼成的三角形的个数为( )
如图,用火柴棍拼成一排由三角形组成的图形,按此规律,如果图形中含有41根火柴棍,则可以拼成的三角形的个数为( )| A. | 20个 | B. | 21个 | C. | 22个 | D. | 3个 |
3.如图,边长为(m+5)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为5,则另一边长是( )
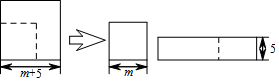

| A. | m+3 | B. | m+5 | C. | 2m+5 | D. | 2m+10 |
4. 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
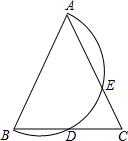 等腰△ABC的顶角∠BAC=50°,以腰AB为直径作半圆,交BC于点D,DE交AC于点E,则$\widehat{DE}$=50°.
等腰△ABC的顶角∠BAC=50°,以腰AB为直径作半圆,交BC于点D,DE交AC于点E,则$\widehat{DE}$=50°.