题目内容
5.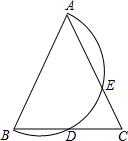 等腰△ABC的顶角∠BAC=50°,以腰AB为直径作半圆,交BC于点D,DE交AC于点E,则$\widehat{DE}$=50°.
等腰△ABC的顶角∠BAC=50°,以腰AB为直径作半圆,交BC于点D,DE交AC于点E,则$\widehat{DE}$=50°.
分析 连接AD,由AB为直径可得出AD⊥BC,由AB=AC利用等腰三角形的三线合一即可得出∠BAD=∠CAD=$\frac{1}{2}$∠BAC=25°,再根据圆周角定理即可得出$\widehat{DE}$的度数.
解答 解:连接AD,如图所示.
∵AB为直径,
∴AD⊥BC.
∵AB=AC,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=25°.
∴$\widehat{DE}$的度数=2∠EAD=50°.
故答案为:50.
点评 此题考查了圆周角定理以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.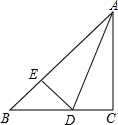 如图,△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,若AB=10cm,AC=6cm,BC=8cm,则△BED的周长为( )
如图,△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,若AB=10cm,AC=6cm,BC=8cm,则△BED的周长为( )
 如图,△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,若AB=10cm,AC=6cm,BC=8cm,则△BED的周长为( )
如图,△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,若AB=10cm,AC=6cm,BC=8cm,则△BED的周长为( )| A. | 10cm | B. | 12cm | C. | 14cm | D. | 16cm |
17.2008年在北京举办了第29届夏季奥运会,观察如表
若用n表示奥运会届数,试用含n的代数式表示相应的举办年份是4n+1892.
| 届数 | 第1届 | 第2届 | 第3届 | … | 第29届 | … |
| 举办年份 | 1896年 | 1900年 | 1904年 | 2008年 |
14.下面四个二次函数解析式中,开口方向不同的那个是( )
| A. | y=2x2-3x+1 | B. | y=(x-5)(x-6) | C. | $y=\frac{1}{2}{({x+1})^2}-3$ | D. | y=x-x2-4 |