题目内容

5．若等腰三角形的周长为20cm，底边长为xcm，一腰长为ycm，则y与x的函数表达式正确的是（　　）
A．y=20-2x（0＜x＜20）B．y=20-2x（0＜x＜10）C．y=$\frac{1}{2}$（20-x）（0＜x＜20）D．y=$\frac{1}{2}$（20-x）（0＜x＜10）

分析 根据等腰三角形的性质和周长公式列出算式，再根据两边之和大于第三边两边之差小于第三边，即可得出函数表达式的取值范围．

解答 解：∵等腰三角形周长为20cm，腰长为ycm，底边为xcm，
∴2y+x=20，
∴y=$\frac{1}{2}$（20-x）（0＜x＜10）．
故选D．

点评 本题考查了根据实际问题列一次函数关系式，用到的知识点是等腰三角形的性质和周长公式，注意函数的取值范围．

练习册系列答案
相关题目
15．大于-3而不大于2的整数有-2、-1、0、1、2．
16．阅读下列材料，并解决后面的问题．
在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c．过A作AD⊥BC于D（如图），
则sinB=$\frac{AD}{c}$，sinC=$\frac{AD}{b}$，即AD=c•sinB，AD=b•sinC，于是c•sinB=b•sinC，即$\frac{b}{sinB}$=$\frac{c}{sinC}$
同理有$\frac{c}{sinC}$=$\frac{a}{sinA}$，$\frac{a}{sinA}$=$\frac{b}{sinB}$
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$…（*）
即：在一个三角形中，各边和它所对角的正弦的比相等．
在锐角三角形中，若已知三个元素a、b、∠A，运用上述结论（*）和有关定理就可以求出其余三个未知元素c、∠B、∠C，请你补全答题卡上的解题思路．
13．计算：cos30°+$\sqrt{3}$tan60°-2sin45°．
20．对于二次函数y=mx2+（5m+3）x+4m（m为常数且m≠0）有以下三种说法：
①不论m为何值，函数图象一定过定点（-1，-3）；
②当m=-1时，函数图象与坐标轴有3个交点；
③当m＜0，x≥-$\frac{67}{26}$时，函数y随x的增大而减小；
判断真假，并说明理由．
10．如图，在△ABC中，点D在线段BC上且∠BAD=∠C，BD=2，CD=6，则AB的值是（　　）
A．12B．8C．4D．3
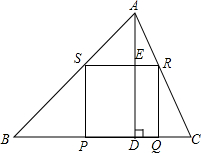17．如图，AD是△ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=30cm，AD=20cm，四边形PQRS是正方形．
（1）求证：AS•BC=AB•SR．
（2）求正方形PQRS的边长．
14．解方程式
（1）x2-2x=0
（2）x2+2x-4=0（用配方法）
（3）2x2+5x-1=0（用公式法）
（4）x2-x-6=0．
15．（1）-3×3n÷3n-2×（-3）-3；
（2）4x2-（-2x+3）（-3-2x）
（3）${（-m-\frac{1}{2}n）^2}$
（4）（a-2b+3c）（a+2b-3c）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网