题目内容
17.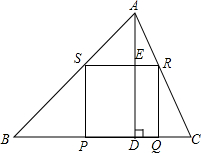 如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=30cm,AD=20cm,四边形PQRS是正方形.
如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=30cm,AD=20cm,四边形PQRS是正方形.(1)求证:AS•BC=AB•SR.
(2)求正方形PQRS的边长.
分析 (1)由四边形PQRS是正方形,可得SR∥BC,即可证得△ASR∽△ABC,然后由相似三角形的对应边成比例,证得结论;
(2)首先设正方形PQRS的边长为xcm,然后由相似三角形对应高的比等于相似比,得方程:$\frac{x}{30}$=$\frac{20-x}{20}$,解此方程即可求得答案.
解答 (1)证明:∵四边形PQRS是正方形,
∴SR∥BC,
∴△ASR∽△ABC,
∴AS:AB=SR:BC,
∴AS•BC=AB•SR.
(2)解:设正方形PQRS的边长为xcm,
∵AD是△ABC的高,SR∥BC,
∴AE是△ASR的高,
则AE=AD-ED=20-x(cm),
∵△ASR∽△ABC,
∴$\frac{SR}{BC}=\frac{AE}{AD}$,
∴$\frac{x}{30}$=$\frac{20-x}{20}$,
解得:x=12,
∴正方形PQRS的边长为12cm.
点评 此题考查了相似三角形的判定与性质以及正方形的性质.注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
8.在Rt△ABC中,∠C=90°,cosA=$\frac{2}{3}$,AB=6,则BC=( )
| A. | 2 | B. | 4 | C. | 6 | D. | $2\sqrt{5}$ |
5.若等腰三角形的周长为20cm,底边长为xcm,一腰长为ycm,则y与x的函数表达式正确的是( )
| A. | y=20-2x(0<x<20) | B. | y=20-2x(0<x<10) | C. | y=$\frac{1}{2}$(20-x)(0<x<20) | D. | y=$\frac{1}{2}$(20-x)(0<x<10) |
12.下列等式中,从等号左边到右边的变形是因式分解的是( )
| A. | x2-9+8x=(x-3)(x+3)+8x | B. | -5x2y3=-5xy•(xy2) | ||
| C. | x2-4x-5=x(x-4-$\frac{5}{x}$) | D. | -x2+2xy=-x(x-2y) |