题目内容
13.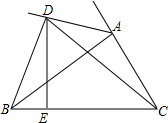 如图,BC=CD,∠BCA-∠ACD=60°,求证:AD+CD≥AB.
如图,BC=CD,∠BCA-∠ACD=60°,求证:AD+CD≥AB.
分析 在四边形ADBC内作∠BCM=60°,CM交AB于N,在射线CM上取一点F,使FB=FC,连接FB,FA,于是得到△FBC是等边三角形,求出CD=BC=FB=FC,由于∠BCA-∠ACD=60°,于是得到∠BCA-60°=∠ACD,即∠FCA=∠ACD,证得△ACF≌△ACD,根据全等三角形的性质得到AF=AD,若F与N不重合,(∠B≠60°),AD+CD>AB,若F与N重合,(∠B=60°),AD+CD=AB,于是得到结论.
解答 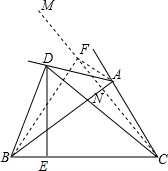 证明:在四边形ADBC内作∠BCM=60°,CM交AB于N,在涉嫌CE上取一点F,使FB=FC,连接FB,FA,
证明:在四边形ADBC内作∠BCM=60°,CM交AB于N,在涉嫌CE上取一点F,使FB=FC,连接FB,FA,
∵FB=FC,∠FCB=60°,
∴△FBC是等边三角形,
∴CD=BC=FB=FC,
∵∠BCA-∠ACD=60°,
∴∠BCA-60°=∠ACD,
即∠FCA=∠ACD,
在△ACF≌△ACD中,
$\left\{\begin{array}{l}{CD=CF}\\{∠FCA=∠ACD}\\{AC=AC}\end{array}\right.$,
∴△ACF≌△ACD,
∴AF=AD,
若F与N不重合,(∠B≠60°),AD+CD>AB,
若F与N重合,(∠B=60°),AD+CD=AB,
综上所述AD+CD≥AB.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
5.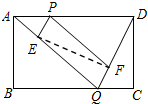 如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
 如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )| A. | y=-$\frac{1}{3}$x2+x | B. | y=-$\frac{2}{3}$x2+2x | C. | y=-$\frac{1}{3}$x2+x+3 | D. | y=-$\frac{2}{3}$x2+2x+6 |
2. 观察下图的规律,在“?”处填上的数字是( )
观察下图的规律,在“?”处填上的数字是( )
 观察下图的规律,在“?”处填上的数字是( )
观察下图的规律,在“?”处填上的数字是( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
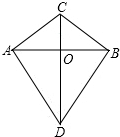 如图,CA=CB,DA=DB.求证:OA=OB,CD⊥AB.
如图,CA=CB,DA=DB.求证:OA=OB,CD⊥AB.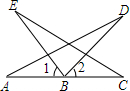 如图,A、B、C在同一条直线上,∠1=∠2,AB=BC,BD=BE.求证:∠D=∠E.
如图,A、B、C在同一条直线上,∠1=∠2,AB=BC,BD=BE.求证:∠D=∠E. 如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.
如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.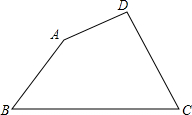 已知:四边形ABCD,∠B=50°,∠C=60°,满足AD+DC=BC,AB2+DC2=4AD2,求:∠A.
已知:四边形ABCD,∠B=50°,∠C=60°,满足AD+DC=BC,AB2+DC2=4AD2,求:∠A.