题目内容
3.先化简,再求值:$\frac{2}{a-1}$+$\frac{a+3}{1-{a}^{2}}$,其中a=2.分析 先根据分式混合运算的法则把原式进行化简,再把a=2代入进行计算即可.
解答 解:原式=$\frac{2(a+1)-a-3}{(a+1)(a-1)}$
=$\frac{2a+2-a-3}{(a+1)(a-1)}$
=$\frac{a-1}{(a+1)(a-1)}$
=$\frac{1}{a+1}$,
当a=2时,原式=$\frac{1}{2+1}$=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.为丰富学生学习生活,学校举行绘画展,小强所绘长为80cm,宽为50cm的图画被选中去参加展览,图画四周镶上一条等宽的金边装裱成一幅矩形挂图后,图画的面积是整个挂图面积的$\frac{20}{27}$.若设金边的宽度为xcm,那么x满足的方程是( )
| A. | $(80+2x)(50+2x)×\frac{20}{27}=80×50$ | B. | $(80+2x)(50+2x)=80×50×\frac{20}{27}$ | ||
| C. | $(80-2x)(50-2x)×\frac{20}{27}=80×50$ | D. | $(80-2x)(50-2x)=80×50×\frac{20}{27}$ |
8.若∠A、∠B为△ABC中的锐角,且$\sqrt{2sinA-\sqrt{3}}$+(cosB-$\frac{1}{2}$)2=0,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 无法确定 |
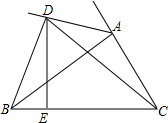 如图,BC=CD,∠BCA-∠ACD=60°,求证:AD+CD≥AB.
如图,BC=CD,∠BCA-∠ACD=60°,求证:AD+CD≥AB.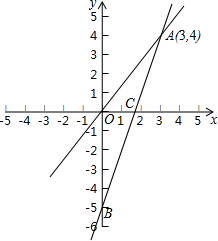 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C. 把2016个正整数1,2,3,4,…,2016按如图方式排列成一个表.
把2016个正整数1,2,3,4,…,2016按如图方式排列成一个表.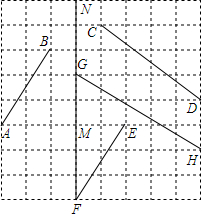 在如图所示的方格纸上,
在如图所示的方格纸上,