题目内容
5．
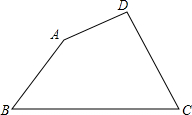已知：四边形ABCD，∠B=50°，∠C=60°，满足AD+DC=BC，AB2+DC2=4AD2，求：∠A．
分析 在BC上取一点E，使CE=CD，得到△CDE是等边三角形，于是得到DE=DC，过E作EF⊥DE，使EF=AB，连接AF，由AB2+DC2=4AD2，得到DF=2AD，求得AF=AD推出△AFE≌△ABE，根据全等三角形的性质得到∠EFA=∠B=50°，由于∠FEB=180°-60°-90°=30°，即可得到结论．
解答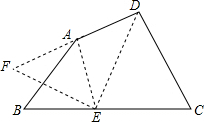 
解：在BC上取一点E，使CE=CD，∵∠C=60°，
∴△CDE是等边三角形，
∴DE=DC，过E作EF⊥DE，使EF=AB，连接AF，
∵AB2+DC2=4AD2，
∴DF=2AD，
∴A是DF的中点，
∴AF=AD，
∴D，A，F三点共线，
∵AF=AD=BC-EC=BE，
在△AFE与△ABE中，
$\left\{\begin{array}{l}{AE=AE}\\{AF=BE}\\{EF=AB}\end{array}\right.$，
∴△AFE≌△ABE，
∴∠EFA=∠B=50°，
∵∠FEB=180°-60°-90°=30°，
∴∠FAB=30°，
∴∠A=180°-30°=150°．
点评 本题考查了全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的性质，三角形的内角和，平角的定义，正确作出辅助线是解题的关键．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
17．制作合适的统计图表示下列信息：
（1）某城市家庭人口数的统计结果为：2口之家占20%，3口之家占50%，4口之家占10%，5口之家占10%，6口之家占5%，其他占5%．
（2）某市“学生上学方式”抽样调查结果如下：
（3）某家媒体公布世界人口数据为：1957年30亿，1974年40亿，1987年50亿，1999年60亿，2013年70亿，预计2025年80亿．
（1）某城市家庭人口数的统计结果为：2口之家占20%，3口之家占50%，4口之家占10%，5口之家占10%，6口之家占5%，其他占5%．
（2）某市“学生上学方式”抽样调查结果如下：
| 上学方式 | 步行 | 骑自行车 | 乘公共汽车 | 其他 |
| 人数 | 30 | 100 | 150 | 20 |
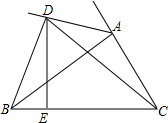如图，BC=CD，∠BCA-∠ACD=60°，求证：AD+CD≥AB．
如图，已知：AD∥BC，点E在DC上，且AE，BE分别平分∠BAD和∠ABC．求证：点E为CD中点．
如图，点A、B、C顺次在直线l上，点M是线段AC的中点，点N是线段BC的中点，NC=2cm，AB=8cm，求AM的长．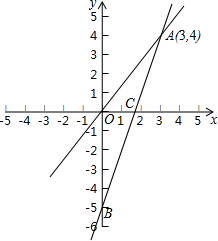
如图，一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A（3，4），且一次函数y2的图象与y轴相交于点B（0，-5），与x轴交于点C．