题目内容
18. 如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.
如图,在等边三角形中,D为BC上一点,BD=2CD,DE⊥AB于E,CE交AD于P.(1)求证:BE=CD;
(2)求△APE的度数.
分析 (1)根据等边三角形的性质得到BC=AC,∠CBE=∠ACD=60°,由DE⊥AB,得到∠BDE=90°-∠CBD=30°,根据直角三角形的性质得到BD=2CD,即可得到结论;
(2)根据已知条件得到△CBE≌△ACD,根据全等三角形的性质得到∠BCE=∠CAD,于是得到∠APE=∠CAD+∠ACP=∠BCE+∠ACP=∠ACB=60°.
解答 (1)证明:∵△ABC是等边三角形,
∴BC=AC,∠CBE=∠ACD=60°,
∵DE⊥AB,
∴∠BDE=90°-∠∠CBD=30°,
∴BD=2CD,
∵BD=2CD,
∴BE=CD;
(2)解:在△CBE和△ACD中,
$\left\{\begin{array}{l}{BE=CD}\\{∠CBE=∠ACD=60°}\\{BC=AC}\end{array}\right.$,
∴△CBE≌△ACD,
∴∠BCE=∠CAD,
∴∠APE=∠CAD+∠ACP=∠BCE+∠ACP=∠ACB=60°,
即∠APE=60°.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.已知函数y=$\frac{k}{x}$的图象过点(1,-2),则该函数的图象必在( )
| A. | 第二、三象限 | B. | 第二、四象限 | C. | 第一、三象限 | D. | 第三、四象限 |
11.甲、乙、丙三人沿圆形操场的某一个固定点出发,甲按顺时针方向走,乙与丙按逆时针方向走,甲第一次遇到乙后又走了30秒遇到丙,再过4分钟第二次遇到乙,已知甲、乙的速度比是3:2,操场的周长是900米,丙的速度是( )米/分.
| A. | 120 | B. | 80 | C. | 60 | D. | 50 |
7.关于x的方程x2+2kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
8.若∠A、∠B为△ABC中的锐角,且$\sqrt{2sinA-\sqrt{3}}$+(cosB-$\frac{1}{2}$)2=0,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 无法确定 |
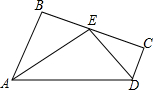 如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证:
如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证: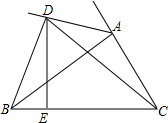 如图,BC=CD,∠BCA-∠ACD=60°,求证:AD+CD≥AB.
如图,BC=CD,∠BCA-∠ACD=60°,求证:AD+CD≥AB.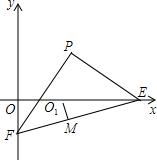 如图,P(1,1),PE⊥PF,O为△OEF的内角平分线的交点,O1M⊥EF于M.
如图,P(1,1),PE⊥PF,O为△OEF的内角平分线的交点,O1M⊥EF于M. 如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点,NC=2cm,AB=8cm,求AM的长.
如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点,NC=2cm,AB=8cm,求AM的长.