题目内容
18．分式方程$\frac{3}{x+5}$-$\frac{1}{x-1}$=0解的情况是（ ）| A． | 有解，x=1 | B． | 有解，x=5 | C． | 有解，x=4 | D． | 无解 |
分析 根据等式的性质，可得整式方程，根据解整式方程，可得答案．
解答 解：两边都乘以（x+5）（x-1），得
3（x-1）-（x+5）=0，
化简，得2x=8
解得x=4，
经检验：x=4是原分式方程的解，
故选：C．
点评 本题考查了分式方程的解，利用等式的性质得出整式方程是解题关键．
练习册系列答案
相关题目
8．下列运算正确的是（ ）
| A． | 2a+3b=5ab | B． | a1•a4=a6 | C． | （a2b）3=a6b3 | D． | （a+2）2=a2+4 |
9．
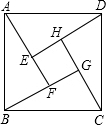如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为（ ）
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为（ ）| A． | $\frac{3}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{{2\sqrt{13}}}{13}$ |
6．用配方法解一元二次方程x2-4x=5时，下列配方正确的是（ ）
| A． | （x-2）2=9 | B． | （x-2）2=1 | C． | （x+2）2=9 | D． | （x+2）2=1 |
13．
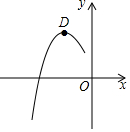已知抛物线y=ax2+bx+c的顶点为D（-1，2），其部分图象如图所示，给出下列四个结论：
①a＜0； ②b2-4ac＞0；③2a-b=0；④若点P（x0，y0）在抛物线上，则ax02+bx0+c≤a-b+c．其中结论正确的是（ ）
已知抛物线y=ax2+bx+c的顶点为D（-1，2），其部分图象如图所示，给出下列四个结论：①a＜0； ②b2-4ac＞0；③2a-b=0；④若点P（x0，y0）在抛物线上，则ax02+bx0+c≤a-b+c．其中结论正确的是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．-$\frac{1}{3}$的倒数是（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |
如图，△ABC中，AB=AC，以AC为直径的⊙O与边AB、BC分别交于点D、E．过E的直线与⊙O相切，与AC的延长线交于点G，与AB交于点F．
11．
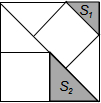有3个正方形按如图所示放置，其中大正方形的边长是1，阴影部分的面积依次记为S1，S2，则S1+S2等于（ ）
有3个正方形按如图所示放置，其中大正方形的边长是1，阴影部分的面积依次记为S1，S2，则S1+S2等于（ ）| A． | $\frac{13}{72}$ | B． | $\frac{13}{36}$ | C． | $\frac{17}{72}$ | D． | $\frac{3}{16}$ |