题目内容
13.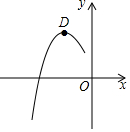 已知抛物线y=ax2+bx+c的顶点为D(-1,2),其部分图象如图所示,给出下列四个结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,2),其部分图象如图所示,给出下列四个结论:①a<0; ②b2-4ac>0;③2a-b=0;④若点P(x0,y0)在抛物线上,则ax02+bx0+c≤a-b+c.其中结论正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用抛物线开口方向可对①进行判断;利用抛物线与x轴的交点个数可对②进行判断;利用顶点坐标得到抛物线的对称轴,然后利用对称轴方程可对③进行判断;利用二次函数的性质可对④进行判断.
解答 解:∵抛物线开口向下,
∴a<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以②正确;
∵抛物线y=ax2+bx+c的顶点为D(-1,2),
∴抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1,
∴b=2a,即2a-b=0,所以③正确;
∵抛物线y=ax2+bx+c的顶点为D(-1,2),
∴x=-1时,y有最大值2,
∴点P(x0,y0)在抛物线上,则ax02+bx0+c≤a-b+c,所以④正确.
故选D.
点评 本题考查了二次函数图象于系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
4.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对某区中小学生的睡眠时间的调查 | |
| B. | 对我市初中学生的兴趣爱好的调查 | |
| C. | 对我市中学教师的健康状况的调查 | |
| D. | 对“天宫二号”飞行器各零部件的质量的调查 |
18.分式方程$\frac{3}{x+5}$-$\frac{1}{x-1}$=0解的情况是( )
| A. | 有解,x=1 | B. | 有解,x=5 | C. | 有解,x=4 | D. | 无解 |
 在“校园读书月”活动中,小华调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图.下面有四个推断:
在“校园读书月”活动中,小华调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图.下面有四个推断:
 已知,矩形ABCD中,AB=10,AD=25,P、Q分别是AB、CD的中点,点O从P点出发,以每秒一个单位的速度,沿着PQ向Q点移动,移动时间为t秒,当到达Q点时停止运动,在运动过程中,以O为圆心,OA长为半径的⊙O与矩形四边的交点个数会出现哪些情况?请直接写出,并指明对应的t的取值范围.
已知,矩形ABCD中,AB=10,AD=25,P、Q分别是AB、CD的中点,点O从P点出发,以每秒一个单位的速度,沿着PQ向Q点移动,移动时间为t秒,当到达Q点时停止运动,在运动过程中,以O为圆心,OA长为半径的⊙O与矩形四边的交点个数会出现哪些情况?请直接写出,并指明对应的t的取值范围.