题目内容
16. 在△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB,E、F分别是AC和BC的中点,求△DEF的周长.
在△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB,E、F分别是AC和BC的中点,求△DEF的周长.
分析 先根据勾股定理得出AB,再由三角形的中位线定理得出EF的长,根据直角三角形斜边上的中线等于斜边的一半得出DE,DF,即可得出△DEF的周长.
解答 解:∵∠ACB=90°,
∴AC2+BC2=AB2,
∵AC=12,BC=5,
∴AB=6.5,
∵E、F分别是AC和BC的中点,
∴EF=$\frac{1}{2}$AB=6.5,
∵CD⊥AB,
∴DE=$\frac{1}{2}$BC=2.5,DF=$\frac{1}{2}$AC=6,
∴△DEF的周长=6.5+2.5+6=15.
点评 本题考查了三角形的中位线定理以及直角三角形的性质,熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
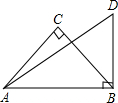 如图所示,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长.
如图所示,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长.