题目内容
6.解方程:x2+(x-$\sqrt{2}$)2=4.分析 先把方程化为一般式,再计算出判别式的值,然后根据求根公式法解方程.
解答 解:x2-$\sqrt{2}$x-2=0,
△=(-$\sqrt{2}$)2-4×(-2)=10,
x=$\frac{\sqrt{2}±\sqrt{10}}{2}$,
所以x1=$\frac{\sqrt{2}+\sqrt{10}}{2}$,x2=$\frac{\sqrt{2}-\sqrt{10}}{2}$.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
例如,用十六进制表示:C+F=1B,19-F=A,18÷4=6,则A×B=( )
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 72 | B. | 6E | C. | 5F | D. | B0 |
15.若-2xm-ny2与3x4y2m+n是同类项,则m-3n的立方根是( )
| A. | 2 | B. | ±2 | C. | -2 | D. | 2$\sqrt{2}$ |
 在△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB,E、F分别是AC和BC的中点,求△DEF的周长.
在△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB,E、F分别是AC和BC的中点,求△DEF的周长. 如图,在△ABC中,BC边的垂直平分线交AB于点E,交BC于点D,若BE2-AE2=AC2.试说明∠A=90°.
如图,在△ABC中,BC边的垂直平分线交AB于点E,交BC于点D,若BE2-AE2=AC2.试说明∠A=90°.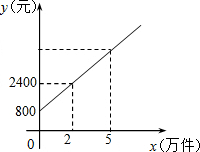 某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:
某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题: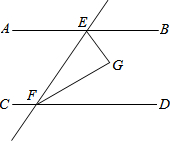 如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.
如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.