题目内容
6.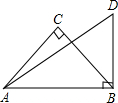 如图所示,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长.
如图所示,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长.
分析 在直角△ABD中,先根据30°角所对的直角边等于斜边的一半得出BD=$\frac{1}{2}$AD=4,再根据勾股定理求出AB=4$\sqrt{3}$,然后解等腰直角△ABC就可以求出AC的长.
解答 解:在直角△ABD中,∵∠ABD=90°,∠DAB=30°,AD=8,
∴BD=$\frac{1}{2}$AD=4,
∴AB=$\sqrt{A{D}^{2}-B{D}^{2}}$=4$\sqrt{3}$.
在直角△ABC中,∵∠ACB=∠ABD=90°,CA=CB,
∴AC=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×4$\sqrt{3}$=2$\sqrt{6}$.
点评 本题主要考查了含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了勾股定理及等腰直角三角形的性质.

练习册系列答案
相关题目
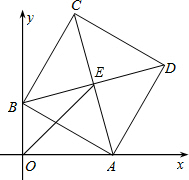 已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.
已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.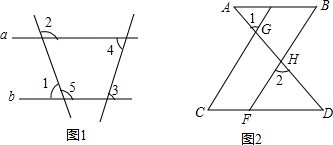 看图填空:
看图填空: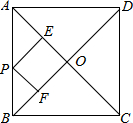 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.
如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5. 在△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB,E、F分别是AC和BC的中点,求△DEF的周长.
在△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB,E、F分别是AC和BC的中点,求△DEF的周长.