Question

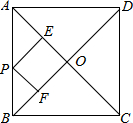
7．已知：正方形ABCD中，点E是对角线AC上一点，EF⊥BC于F，EG⊥CD于点G
（1）如图1，试确定AE与DG的关系AE=$\sqrt{2}$DG．
（2）将四边形EFCG绕点C顺时针旋转一定角度α．
①如图2，AE与DG的数量关系与（1）中比较是否发生变化？试说明理由．
②当0°＜α＜360°时，直线BE与直线CD交于点M，若只考虑线段BE与线段CD相交和BE的延长线与DC的延长线相交的情况，则当α为多少度时S_△BNC=S_△DME（直接写出答案）

Answer 1

分析 （1）过点E作EP⊥AD，根据矩形EGDP得出EP=DG，再根据正方形的性质得出AE=$\sqrt{2}$EP，可得AE与DG的关系；
（2）根据正方形的性质，再证明△ACE∽△DCG，进而得出AE与DG的关系不变化即可；
（3）通过作出旋转的图示，即可得出当S_△BNC=S_△DME时，旋转的角度是90°和270°．

解答 解：（1）过点E作EP⊥AD，如图1，

∵正方形ABCD，
∴∠ACD=∠AFP=45°，
∴AE=$\sqrt{2}$PE，
∵PE=DG，
∴AE=$\sqrt{2}$DG；
故填：AE=$\sqrt{2}$DG；
（2）不变化，理由如下：
∵四边形ABCD和四边形EFCG是正方形，
∴∠ACD=∠ECG=45°，
∴∠ACD-∠ECD=∠ECG-∠ECD，
即∠ACE=∠DCG，
∵在正方形ABCD和正方形EFCG中，
AC=$\sqrt{2}$CD，EC=$\sqrt{2}$CG，
∴$\frac{AC}{DC}=\frac{EC}{GC}=\sqrt{2}$，
∴△ACE∽△DCG，
∴$\frac{AC}{DC}=\frac{EC}{GC}=\frac{AE}{DG}=\sqrt{2}$，
即AE=$\sqrt{2}$DG；
（3）当线段BE与线段CD相交交于点M，此时四边形EFCG绕点C顺时针旋转的角度α为90°，如图2，

∵正方形ABCD和正方形EFCG，
∴BC=CD，EF=CF，
∴S_△BCE=S_△DCE，
∴S_△BCE-S_△CME=S_△DCE-S_△CME，
∴S_△BCM=S_△DME；
当BE的延长线与DC的延长线相交点N时，此时四边形EFCG绕点C顺时针旋转的角度α为270°，如图3，

∵正方形ABCD和正方形EFCG，
∴BC=CD，EF=CF，
∴S_△BCE=S_△DCE，
∴S_△BCE-S_△CNE=S_△DCE-S_△CNE，
∴S_△BCN=S_△DNE．

点评 此题考查相似三角形的判定与性质和正方形的性质，关键是根据旋转的性质分析解答．注意旋转的两种情况分析．