题目内容
3.化简(1)$\frac{{3{a^2}b}}{6ab}$
(2)$\frac{2a}{{a}^{2}-4}$-$\frac{1}{a+2}$
(3)[$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$-$\frac{a}{{a}^{2}-a}$]÷$\frac{a}{a-2}$.
分析 (1)可以分子分母约分解答本题;
(2)根据分式的减法可以解答本题;
(3)先化简括号内的式子,然后根据分式的除法即可解答本题.
解答 解:(1)$\frac{{3{a^2}b}}{6ab}$=$\frac{a}{2}$;
(2)$\frac{2a}{{a}^{2}-4}$-$\frac{1}{a+2}$
=$\frac{2a-(a-2)}{(a+2)(a-2)}$
=$\frac{a+2}{(a+2)(a-2)}$
=$\frac{1}{a-2}$;
(3)[$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$-$\frac{a}{{a}^{2}-a}$]÷$\frac{a}{a-2}$
=$(\frac{a+1}{a-1}-\frac{1}{a-1})×\frac{a-2}{a}$
=$\frac{a}{a-1}×\frac{a-2}{a}$
=$\frac{a-2}{a-1}$.
点评 本题考查分式的混合运算,解答本题的关键是明确分式混合运算的计算方法.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.点M(2,-3)到x轴的距离是( )
| A. | 2 | B. | -3 | C. | 3 | D. | 以上都不对 |
8.一次函数y=$\frac{4}{3}$x-b沿y轴平移3个单位得直线与y=$\frac{4}{3}$x-1,则b的值为( )
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
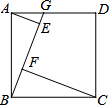 如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=16.
如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2=16. 如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,请你利用方程组的思想方法求出图中阴影部分面积是多少cm2?
如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,请你利用方程组的思想方法求出图中阴影部分面积是多少cm2?