��Ŀ����
13����ͼ����ֱ֪��y=mx+n�뷴��������y=$\frac{k}{x}$����A��B���㣬��A�ڵ�B����ߣ���x�ᡢy��ֱ�C����D��AE��x����E��BF��y����F����1����m=k��n=0����A��B����������ꣻ
��2����ͼ1����A��x1��y1����B��x2��y2����д��y1+y2��n�Ĵ�С��ϵ����֤����
��3����ͼ2��M��N�ֱ�Ϊ����������y=$\frac{b}{x}$ͼ���ϵĵ㣬AM��MN��x�ᣮ��$\frac{1}{AM}$+$\frac{1}{BN}$=$\frac{5}{3}$����AM��BN֮��ľ���Ϊ5����k-b=3��
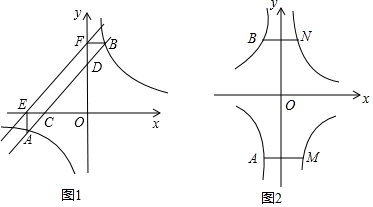
���� ��1����$\left\{\begin{array}{l}{y=kx}\\{y=\frac{k}{x}}\end{array}\right.$��ã�$\left\{\begin{array}{l}{x=1}\\{y=k}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-k}\end{array}\right.$�����ɵó��𰸣�
��2������A��x1��y1����B��x2��y2������y=mx+n�ó�y1+y2=m��x1+x2��+2n����$\left\{\begin{array}{l}{y=mx+n}\\{y=\frac{k}{x}}\end{array}\right.$�ó�mx2+nx-k=0���ɸ���ϵ����ϵ�ó�x1+x2=-$\frac{n}{m}$���ó�y1+y2=n���ɣ�
��3����A��x1��y1����B��x2��y2������M��x3��y1����N��x4��y2�����ɷ����������ó�x1y1=x2y2=k��x3y1=x4y2=b����������ͼ�����ʵó�AM=x3-x1=$\frac{b}{{y}_{1}}$-$\frac{k}{{y}_{1}}$=$\frac{b-k}{{y}_{1}}$��bn=x2-x4=$\frac{k}{{y}_{2}}$-$\frac{b}{{y}_{2}}$=$\frac{k-b}{{y}_{2}}$��y2-y1=5���ٽ����֪���������ɵó��𰸣�
��� �⣺��1����$\left\{\begin{array}{l}{y=kx}\\{y=\frac{k}{x}}\end{array}\right.$��ã�$\left\{\begin{array}{l}{x=1}\\{y=k}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-k}\end{array}\right.$��
��A��1��k����B��-1��-k����
��2��y1+y2=n���������£�
����A��x1��y1����B��x2��y2������y=mx+n��
��y1=mx1+n��y2=mx2+n��
��y1+y2=m��x1+x2��+2n��
��$\left\{\begin{array}{l}{y=mx+n}\\{y=\frac{k}{x}}\end{array}\right.$�ã�mx+n=$\frac{k}{x}$��
��mx2+nx-k=0��
��ֱ��y=mx+n�뷴��������y=$\frac{k}{x}$����A��B���㣬
��x1+x2=-$\frac{n}{m}$��
��y1+y2=m•��-$\frac{n}{m}$��+2n=-n+2n=n��
��3����A��x1��y1����B��x2��y2����
��AM��MN��x�ᣮ��M��x3��y1����N��x4��y2����
��x1y1=x2y2=k��x3y1=x4y2=b��AM=x3-x1=$\frac{b}{{y}_{1}}$-$\frac{k}{{y}_{1}}$=$\frac{b-k}{{y}_{1}}$��bn=x2-x4=$\frac{k}{{y}_{2}}$-$\frac{b}{{y}_{2}}$=$\frac{k-b}{{y}_{2}}$��y2-y1=5��
��$\frac{1}{AM}$+$\frac{1}{BN}$=$\frac{5}{3}$��
��$\frac{{y}_{1}}{b-k}$+$\frac{{y}_{2}}{k-b}$=$\frac{5}{3}$��
��$\frac{{y}_{2}-{y}_{1}}{k-b}$=$\frac{5}{3}$��
��$\frac{5}{k-b}$=$\frac{5}{3}$��
��k-b=3��
�ʴ�Ϊ��3��
���� �����Ƿ����������ۺ���Ŀ�������˷�����������Ӧ�á�������ͼ�����ʡ�������Ľⷨ������ϵ����ϵ��֪ʶ�������ۺ���ǿ����һ���Ѷȣ�

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�| A�� | x=4 | B�� | x=3 | C�� | x=2 | D�� | x=0 |
| A�� | a��1 | B�� | a��1 | C�� | a��2 | D�� | -1��a��2 |
 ��ͼ�����������в����ж�AB��CD���ǣ�������
��ͼ�����������в����ж�AB��CD���ǣ�������| A�� | ��1=��5 | B�� | ��3=��4 | C�� | ��3=��5 | D�� | ��2+��4=180�� |
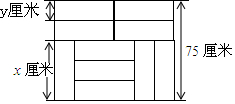 ��ͼ��10����ͬ�ij�����ǽשƴ��һ�����Σ��賤����ǽש�ij��Ϳ��ֱ�Ϊx����y���ף����������з�������ȷ���ǣ�������
��ͼ��10����ͬ�ij�����ǽשƴ��һ�����Σ��賤����ǽש�ij��Ϳ��ֱ�Ϊx����y���ף����������з�������ȷ���ǣ�������| A�� | $\left\{\begin{array}{l}{x+2y=75}\\{y=3x}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{2x+y=75}\\{x=3y}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{2x+y=75}\\{y=3x}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x+2y=75}\\{x=3y}\end{array}\right.$ |
| A�� | 0.6579��103 | B�� | 6.579��102 | C�� | 6.579��106 | D�� | 65.79��105 |
| A�� | 1.796��106 | B�� | 17.96��106 | C�� | 1.796��107 | D�� | 0.1796��107 |
| A�� | 4.233��103Ԫ | B�� | 0.4233��104Ԫ | C�� | 42.33��1010Ԫ | D�� | 4.233��1011Ԫ |