题目内容
7．${（1-\sqrt{2}）^{2007}}•{（1+\sqrt{2}）^{2008}}$=-1-$\sqrt{2}$．分析 先根据积的乘方得到原式=[（1-$\sqrt{2}$）（1+$\sqrt{2}$）]2007•（1+$\sqrt{2}$），然后利用平方差公式计算．
解答 解：原式=[（1-$\sqrt{2}$）（1+$\sqrt{2}$）]2007•（1+$\sqrt{2}$）
=（1-2）2007•（1+$\sqrt{2}$）
=-1-$\sqrt{2}$．
故答案为-1-$\sqrt{2}$．
点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．
练习册系列答案
全程金卷系列答案
相关题目
如图，将△ABC沿CB边向右平移得到△DFE，DE交AB于点G．已知∠A：∠C：∠ABC=1：2：3，AB=9 cm，BF=4 cm，AG=5 cm，则图中阴影部分的面积为26cm2．
2．下列各式中，运算正确的是（ ）
| A． | a6÷a3=a2 | B． | $3\sqrt{\frac{a}{3}}=\sqrt{a}$ | C． | $2\sqrt{2}+3\sqrt{3}=5\sqrt{5}$ | D． | $\sqrt{6}÷\sqrt{3}=\sqrt{2}$ |
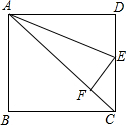如图，已知正方形ABCD的边长为1，以AE为折痕使点D落在AC上F处，求DE的长．