��Ŀ����
3����֪����ͼ��������y=ax2+bx-3��x�ύ��A��B���㣬��y�ύ�ڵ�C��O������ԭ�㣬��֪��B�������ǣ�3��0����tan��OAC=3��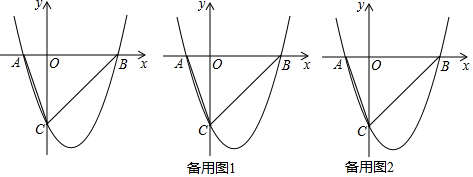
��1����������ߵĺ�������ʽ��
��2����P��x���Ϸ����������ϣ��ҡ�PAB=��CAB�����P�����ꣻ
��3����ƽ����x���ֱ���������߽��ڵ�M��N��M����N����ࣩ��
������MNΪֱ����Բ��x�����У����Բ�İ뾶��
����Q��m��4����ֱ��MN��һ���㣬���Ե�C��B��QΪ����������ε��������6ʱ����ֱ��д������������mֵ��Ϊ3��11��
���� ��1������õ�B�͵�A�����꣬Ȼ��A�͵�B��������������ߵĽ���ʽ�����a��b��ֵ���ɣ�
��2���������֪tan��PAB=3�����P�ĺ�����Ϊx�����P��������Ϊ3��x+1����Ȼ��P��������������ߵĽ���ʽ��⼴�ɣ�
��3������������ߵĶԳ���Ϊx=1���ٵ�ֱ��MN��x���Ϸ�ʱ����Բ�İ뾶ΪR��R��0������N��R+1��R��������N��������������ߵĽ���ʽ�����R��ֵ����ֱ��MN��x���·�ʱ����Բ�İ뾶Ϊr��r��0����N��r+1��-r��������N��������������ߵĽ���ʽ�����r��ֵ���������BC�Ľ���ʽ��BC�ij���Ȼ�����������ε������ʽ�����BC���ϵĸ��߳�Ϊ2$\sqrt{2}$��Ȼ�����ֱ��BC��y=4�Ľ���D�����꣬����Q�ڵ�D�����ʱ������Q��QE��BC����EQ=2$\sqrt{2}$��Ȼ���ڡ�QDE�У���������������Ǻ���ֵ�����QD�ij����ɵõ���Q�����꣬ͬ������Q�ڵ�D���Ҳ�ʱ������õ�Q������꣬�ʴ˿����m��ֵ��
��� �⣺��1����������y=ax2+bx-3��y�ύ�ڵ�C��
���C��������0��-3����
��OC=3��
��tan��OAC=3��
��OA=1������A��������-1��0����
����A�͵�B���������ã�$\left\{\begin{array}{l}{a-b-3=0}\\{9a+3b-3=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$��
�������ߵĺ�������ʽ��y=x2-2x-3��
��2���ߡ�PAB=��CAB��
��tan��PAB=tan��CAB=3��
�ߵ�P��x���Ϸ������P�ĺ�����Ϊx�����P��������Ϊ3��x+1����
��3��x+1��=x2-2x-3����x=-1����ȥ����x=6����x=6ʱ��y=21��
���P��������6��21����
��3����y=x2-2x-3=��x-1��2-4��
�������ߵĶԳ���Ϊֱ��x=1��
�ٵ�ֱ��MN��x���Ϸ�ʱ����Բ�İ뾶ΪR��R��0������N��R+1��R����
��R=�� R+1-1��2-4����ã�R=$\frac{1��\sqrt{17}}{2}$����ֵ��ȥ����
��R=$\frac{1+\sqrt{17}}{2}$��
��ֱ��MN��x���·�ʱ����Բ�İ뾶Ϊr��r��0����
��N��r+1��-r����
��-r=��r+1-1��2-4����ã�r=$\frac{-1��\sqrt{17}}{2}$����ֵ��ȥ����
��r=$\frac{-1+\sqrt{17}}{2}$��
��Բ�İ뾶Ϊ��$\frac{1+\sqrt{17}}{2}$��$\frac{-1+\sqrt{17}}{2}$��
����ֱ��BC�Ľ���ʽΪy=kx+b������C�͵�B���������ã�$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$��
���k=1��b=-3��
��ֱ��BC�Ľ���ʽΪy=x-3��
���ɶ�����֪��BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=3$\sqrt{2}$��
�ߡ�QCB�����Ϊ6��
��BC���ϵĸ��ߵij���=$\frac{6��2}{3\sqrt{2}}$=2$\sqrt{2}$��
��ͼ1��ʾ����ֱ��BC��y=4�Ľ���ΪD������Q�ڵ�D�����ʱ������Q��QE��BC����EQ=2$\sqrt{2}$
��y=0�����ֱ��BC�Ľ���ʽ�ã�x-3=4�����x=7��
���D��������7��4����
��QD��x�ᣬ
���QDC=��OBC=45�㣮
��QD=$\sqrt{2}$QE=$\sqrt{2}$��2$\sqrt{2}$=4��
��Q��3��4����
��m=3��
��ͼ1��ʾ����Qλ�ڵ�D���Ҳ�ʱ��Q�䴦��������Q����Q��F��BC������ΪF����FQ=2$\sqrt{2}$��
ͬ����֪��DQ��=4��
���Q���������11��4����
��m=11��
����������m��ֵΪ3��11��
�ʴ�Ϊ��3��11��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ�����ߵ����ʡ����κ����ĶԳ��ԣ�����������Ǻ���ֵ��Ӧ�ã������ε������ʽ�����������ǽ����Ĺؼ���

| A�� | a��2 | B�� | a��2 | C�� | a��2��a��1 | D�� | a��-2 |
| A�� | $\frac{360}{x}$=$\frac{480}{140-x}$ | B�� | $\frac{480}{x}$=$\frac{360}{140-x}$ | C�� | $\frac{360}{x}$+$\frac{480}{x}$=140 | D�� | x+$\frac{360x}{480}$=140 |
 ��ͼ���ڡ�ABC���У���BAC=90�㣬��AD�۵���ABC��ʹ��Bǡ������AC���ϵĵ�E��������C=20�㣬���ADE=65�㣮
��ͼ���ڡ�ABC���У���BAC=90�㣬��AD�۵���ABC��ʹ��Bǡ������AC���ϵĵ�E��������C=20�㣬���ADE=65�㣮 ��ͼ����ֱ������ϵ�У�A��0��4����B��-2��0����C��2��0����
��ͼ����ֱ������ϵ�У�A��0��4����B��-2��0����C��2��0����