题目内容
18. 如图,在△ABC,中,∠BAC=90°,沿AD折叠△ABC,使点B恰好落在AC边上的点E处,若∠C=20°,则∠ADE=65°.
如图,在△ABC,中,∠BAC=90°,沿AD折叠△ABC,使点B恰好落在AC边上的点E处,若∠C=20°,则∠ADE=65°.
分析 根据直角三角形的性质求出∠B的度数,根据翻折变换的性质求出∠EAD和∠AED的度数,根据三角形内角和定理求出∠ADE即可.
解答 解:在△ABC中,∠CAB=90°,∠C=20°,
∴∠B=90°-∠C=70°.
由折叠的性质可得:∠EAD=$\frac{1}{2}$∠CAB=45°,∠AED=∠B=70°,
∴∠ADE=180°-∠EAD-∠AED=65°.
故答案为:65°.
点评 本题考查的是翻折变换、直角三角形的性质和三角形内角和定理,理解翻折变换的性质、熟记三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
6.中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:

(1)根据上图填写下表:
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.

(1)根据上图填写下表:
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲班 | 8.5 | 8.5 | 8.5 | ,0.7 |
| 乙班 | 8.5 | 8 | 10 | 1.6 |
10.有x辆客车,若每辆客车乘50人,则还有10人不能上车,若每辆车乘52人,则车上只剩2个空位,下列方程中正确的是( )
| A. | 50x-10=52x-2 | B. | 50x+10=52x-2 | C. | 50x+10=52x+2 | D. | 50x-10=52x+2 |
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).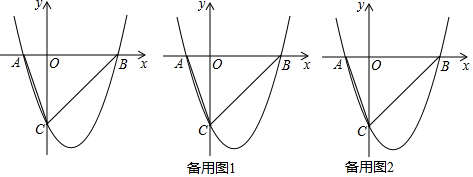
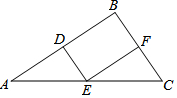 如图,四边形BDEF是直角三角形ABC的内接正方形,如果AB=6,BC=4,求此内接正方形的边长DE.
如图,四边形BDEF是直角三角形ABC的内接正方形,如果AB=6,BC=4,求此内接正方形的边长DE.