题目内容
19.在由6个边长为1的小正方形组成的方格中:(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)
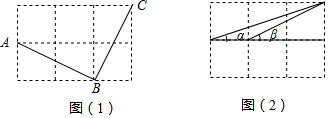
分析 (1)如图(1),根据勾股定理,判断出AB2+BC2=AC2,即可推得△ABC是直角三角形,据此判断出AB与BC的关系,并说明理由即可.
(2)如图(2),根据勾股定理,判断出AB2+BC2=AC2,即可推得△ABC是等腰直角三角形,据此求出∠α+∠β的度数是多少即可.
解答 解:(1)如图(1),连接AC,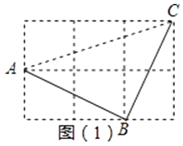 ,
,
由勾股定理得,AB2=12+22=5,
BC2=12+22=5,
AC2=12+32=10,
∴AB2+BC2=AC2,AB=BC,
∴△ABC是直角三角形,∠ABC=90°,
∴AB⊥BC
∴AB与BC是垂直且相等.
(2)∠α+∠β=45°.
证明:如图(2),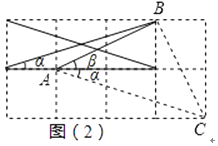 ,
,
由勾股定理得,AB2=12+22=5,
BC2=12+22=5,
AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠α+∠β=45°.
点评 此题主要考查了作图-应用与设计作图,以及勾股定理的应用,要熟练掌握.

练习册系列答案
相关题目
 如图,在△ABC中,BE⊥AC,CD⊥AB,且BD=CE,求证:AB=AC.
如图,在△ABC中,BE⊥AC,CD⊥AB,且BD=CE,求证:AB=AC.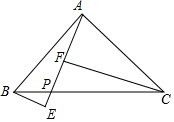 如图,已知在△ABC中,∠BAC=90°,AB=AC,点P为BC边上一动点(BP<CP),分别过B、C作BE⊥AP于点E,CF⊥AP于点F,试说明:EF=CF-BE.
如图,已知在△ABC中,∠BAC=90°,AB=AC,点P为BC边上一动点(BP<CP),分别过B、C作BE⊥AP于点E,CF⊥AP于点F,试说明:EF=CF-BE.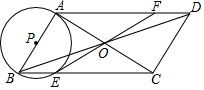 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F.
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F. 如图,已知点E在正方形ABCD在内,AE=6,BE=8,AB=10,求图中阴影部分的面积S.
如图,已知点E在正方形ABCD在内,AE=6,BE=8,AB=10,求图中阴影部分的面积S.